
【题目】粮库6天内粮食进出库的吨数如下(“+”表示进库“-”表示出库)
+25, +8,-12,+34,-36,-22.
(1)经过这6天,粮库里的粮食是增多还是减少了?通过计算说明.
(2)经过这6天,仓库管理员结算发现库里还存480吨粮,那么6天前库里存粮多少吨?
(3)如果进出的装卸费都是每吨5元,那么这6天要付多少装卸费?
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某服装厂生产一种夹克和T恤,夹克每件定价120元,T恤每件定价60元.厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件T恤;②夹克和T恤都按定价的80%付款.现某客户要到该服装厂购买夹克30件,T恤![]() 件(
件(![]() >30).
>30).
(1)若该客户按方案①购买,需付款 元(用含x的代数式表示);
若该客户按方案②购买,需付款 元(用含x的代数式表示);
(2)若![]() =40,通过计算说明按方案①、方案②哪种方案购买较为合算?
=40,通过计算说明按方案①、方案②哪种方案购买较为合算?
(3)若两种优惠方案可同时使用,当![]() =40时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并说明理由.
=40时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.

(1)求证:△BDG∽△DEG;
(2)若EGBG=4,求BE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为 x(h),两车之间的距离为 y(km),图中的折线表示y与x之间的函数关系.根据题中所给信息解答以下问题:
(1)甲、乙两地之间的距离为______ km ;图中点 C 的实际意义为:______;慢车的速度为______,快车的速度为______;
(2)求线段 BC 所表示的 y 与 x 之间的函数关系式;(3)若在第一列快车与慢车相遇时,第二列快车从乙地出发驶往甲地,速度与第一列快车相同.求第二列快车出发多长时间,与慢车相距200km.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,CE⊥AB交AB延长线于点E,点F为点B关于CE的对称点,连接CF,分别延长DC,CF至点G,H,使FH=CG,连接AG,DH交于点P.
(1)依题意补全图1;
(2)猜想AG和DH的数量关系并证明;
(3)若∠DAB=70°,是否存在点G,使得△ADP为等边三角形?若存在,求出CG的长;若不存在,说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形纸片ABCD中,AB=2,BC=3.
操作:将矩形纸片沿EF折叠,使点B落在边CD上.
探究:(1)如图1,若点B与点D重合,你认为△EDA1和△FDC全等吗?如果全等,请给出证明,如果不全等,请说明理由;
(2)如图2,若点B与CD的中点重合,请你判断△FCB1、△B1DG和△EA1G之间的关系,如果全等,只需写出结果,如果相似,请写出结果和相应的相似比;
(3)如图2,请你探索,当点B落在CD边上何处,即B1C的长度为多少时,△FCB1与△B1DG全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个二元一次方程ax+by=c(a,b,c,为常数,且A,B均不为0)有无数组解,我们规定,将其每一个解中x,y的值分别作为一个点的横,纵坐标极点在平面直角坐标系中,这样我们就得到了二元一次方程的图象:一条直线,既二元一次方程的解均满足其对应直线上点的坐标,反之直线上点的坐标均为其对应的二元一次方程的解,即2x-y=0,其中一解x=1,y=2,则对应其图象上一个点(1,2).
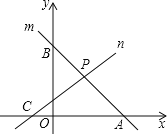
(1)如图,3x+3y=12,的图象为直线m,其与x轴交点A的坐标为____,其与y轴交点B的坐标为___;
(2)如图,ax+by=-5的图象为直线n,其与x轴交于C(-![]() ,0),与(1)中直线m交于P,若P的横坐标为1,求a和b的值.
,0),与(1)中直线m交于P,若P的横坐标为1,求a和b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
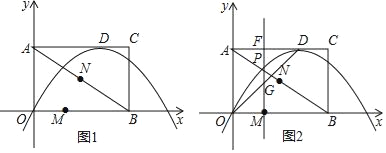
【题目】如图所示,在平面直角坐标系中,矩形AOBC的两边与坐标轴重合,且OB=4,AO=3,若AD=3DC,以D为顶点的抛物线过原点.点M、N为动点,设运动时间为t秒.
(1)求抛物线的解析式;
(2)在图1中,若点M在线段OB上从点O向点B以1个单位/秒的速度运动,同时,点N在线段BA上从点B向点A以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△BMN为直角三角形?
(3)在图2中,过点M做y轴的平行线,分别交抛物线和线段OD于P、G两点,当t为何值时,△ODP的面积最大?最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com