
【题目】观察下面三行数:
-3,9,-27,81…①
1,-3,9,-27…②
-2,10,-26,82…③
(1)按第①行数排列的规律,第5个数是 .
观察第②行数与第①行数的关系,第②行第n个数是 (用含n的式子表示)
观察第③行数与第①行数的关系,第③行第n个数是 (用含n的式子表示)
(2)取每行数的第7个数,计算这三个数的和.
【答案】(1)-243;(-3)n-1;(-3)n+1;(2)-3644.
【解析】
(1)观察可看出第一行的数分别是-3的1次方,二次方,三次方,四次方…且偶数项是正数,奇数项是负数,用式子表示规律为:(-3)n;
(2)观察②,③两行的数与第①行的联系,即可得出答案;
(3)分别求得第①②③行的2012个数,得出x,y,z代入求得答案即可.
解:(1)∵-3,9,-27,81,-243,729…;
∴第①行数是:(-3)1,(-3)2,(-3)3,(-3)4,…(-3)n;
故第5个数是-243.
第②行数是第①行数相应的数乘-![]() ,所以第②行第n个数是-
,所以第②行第n个数是-![]() ×(-3)n,
×(-3)n,
即(-3)n-1.
第③行数的比第①行相应的数大1即(-3)n+1.
(2)第①行中第7个数是(-3)7,第②行中第7个数是(-3)6, 第③行中第7个数是(-3)7+1,所以这三个数的和=(-3)7+(-3)6+(-3)7+1=-3644


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】无锡水蜜桃享誉海内外,老王用3000元购进了一批水蜜桃.第一天,很快以比进价高40% 的价格卖出150千克.第二天,他发现剩余的水蜜桃卖相已不太好,于是果断地以比进价低20%的价格将剩余的水蜜桃全部售出,本次生意老王一共获利750元.
(1)根据以上信息,请你编制一个问题,并给予解答;
(2)老王用3000元按第一次的价格又购进了一批水蜜桃.第一天同样以比进价高40% 的价格卖出150千克,第二天,老王把卖相不好的水蜜桃挑出,单独打折销售,售价为10元/千克,结果很快被一抢而空,其余的仍按第一天的价格销售,且当天全部售完.若老王这次至少获利1100元,请问打折销售的水蜜桃最多多少千克?(精确到1千克.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在电器进入销售旺季,福清某电器超市销售每台进价分别为![]() 元、
元、![]() 元的
元的![]() 两种型号的电器,下表是近两周的销售情况:(进价、售价均保持不变,利润=销售收入-进货成本)
两种型号的电器,下表是近两周的销售情况:(进价、售价均保持不变,利润=销售收入-进货成本)
销售时段 | 销售数量 | 销售收入 | |
|
| ||
第一周 |
|
|
|
第二周 |
|
|
|
(1)求![]() 两种型号的电器销售单价;
两种型号的电器销售单价;
(2)若超市准备用不超过![]() 元的金额再采购这种型号的电器共
元的金额再采购这种型号的电器共![]() 台,销售完这
台,销售完这![]() 台电器实现利润超过
台电器实现利润超过![]() 元的目标,请给出相应的采购方案;并求出利润的最大值.
元的目标,请给出相应的采购方案;并求出利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为节约水资源,制定了新的居民用水收费标准.按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.
(1)求y关于x的函数解析式;
(2)若某用户二、三月份共用水40m3(二月份用水量不超过25m3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形纸片ABCD中,AB=2,BC=3.
操作:将矩形纸片沿EF折叠,使点B落在边CD上.
探究:(1)如图1,若点B与点D重合,你认为△EDA1和△FDC全等吗?如果全等,请给出证明,如果不全等,请说明理由;
(2)如图2,若点B与CD的中点重合,请你判断△FCB1、△B1DG和△EA1G之间的关系,如果全等,只需写出结果,如果相似,请写出结果和相应的相似比;
(3)如图2,请你探索,当点B落在CD边上何处,即B1C的长度为多少时,△FCB1与△B1DG全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列叙述正确的是( )
A. 符号不同的两个数是互为相反数
B. 一个有理数的相反数一定是负有理数
C. 2![]() 与2.75都是﹣
与2.75都是﹣![]() 的相反数
的相反数
D. 0没有相反数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的奇数 1,3,5,7,9,…,排成如图的数阵.
(1)十字框中的五个数的和与中间数 15 有什么关系?
(2)设中间数为 a,用式子表示十字框中五个数之和;
(3)十字框中五个数之和能等于 2 005 吗?若能,请写出这五个数;若不能, 说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)过以下三个点:(m,n),(m+2,2n),和(m+6,n),当抛物线上另有点的横坐标为m+4时,它的纵坐标为_____;当横坐标为m﹣2时,它的纵坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
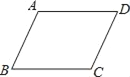
【题目】如图,已知ABCD.
(1)用直尺和圆规在BC边上取一点E,使AB=AE,连结AE;(保留作图痕迹,不写作法)
(2)在(1)的前提下,求证:AE=CD;∠EAD=∠D;
(3)若点E为BC的中点,连接BD,交AE于F,直接写出EF:FA的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com