
【题目】如图,已知ABCD.
(1)用直尺和圆规在BC边上取一点E,使AB=AE,连结AE;(保留作图痕迹,不写作法)
(2)在(1)的前提下,求证:AE=CD;∠EAD=∠D;
(3)若点E为BC的中点,连接BD,交AE于F,直接写出EF:FA的值.
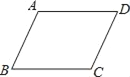
【答案】(1)见解析(2)证明见解析(3)1:2
【解析】分析:(1)以点A为圆心,AB为半径作圆,该圆与BC的交点即为所求的点E;(2)根据平行四边形的对边互相平行可得AD∥BC,再根据两直线平行,内错角相等可得∠AEB=∠EAD,根据等边对等角可得∠ABE=∠AEB,即可得证;(3)由四边形ABCD是平行四边形,可证得△BEF∽△AFD即可求得EF∶FA的值。
详解:(1)如图所示:
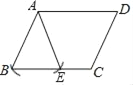 ;
;
(2)证明:在平行四边形ABCD中,AD∥BC,
∴∠AEB=∠EAD,
∵AE=AB,
∴∠ABE=∠AEB,
∴∠B=∠EAD,
∵∠B=∠D,
∴∠DAE=∠D;
(3)解:∵四边形ABCD是平行四边形,
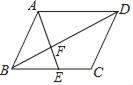
∴AD∥BC,AD=BC,
∴△BEF∽△AFD,
∴![]() =
=![]() ,
,
∵E为BC的中点,
∴BE=![]() BC=
BC=![]() AD,
AD,
∴EF:FA=1:2.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:初中数学 来源: 题型:
【题目】观察下面三行数:
-3,9,-27,81…①
1,-3,9,-27…②
-2,10,-26,82…③
(1)按第①行数排列的规律,第5个数是 .
观察第②行数与第①行数的关系,第②行第n个数是 (用含n的式子表示)
观察第③行数与第①行数的关系,第③行第n个数是 (用含n的式子表示)
(2)取每行数的第7个数,计算这三个数的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
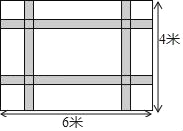
【题目】如图,一块长6米宽4米的地毯,为了美观设计了两横两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的![]() .
.
(1)求配色条纹的宽度;
(2)如果地毯配色条纹部分每平方米造价200元,其余部分每平方米造价100元,求地毯的总造价.(供参考数据:1052=11025,1152=13225,1252=15625)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=![]() ,则△CEF的周长为( )
,则△CEF的周长为( )
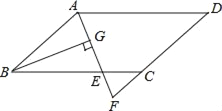
A. 8 B. 9.5 C. 10 D. 11.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法中错误的是( )
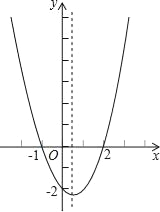
A. 函数有最小值 B. 对称轴是直线x=![]()
C. 当﹣1<x<2时,y<0 D. 当x>![]() 时,y随x的增大而增大
时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张同学在计算![]() 时,将“
时,将“![]() ”错看成了“
”错看成了“![]() ”,得出的结果是
”,得出的结果是![]() .
.
(1)请你求出这道题的正确结果;
(2)试探索:当字母![]() 、
、![]() 满足什么关系时,(1)中的结果与字母
满足什么关系时,(1)中的结果与字母![]() 的取值无关.
的取值无关.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD(纸片)折叠,使点B与AD边上的点K重合,EG为折痕;点C与AD边上的点K重合,FH为折痕.已知∠1=67.5°,∠2=75°,EF=![]() +1,求BC的长.
+1,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间的甲、乙两名工人分别同时生产同种零件,他们一天生产零件y(个)与生产时间t(小时)的关系如图所示.
(1)根据图象回答:
①甲、乙中,谁先完成一天的生产任务;在生产过程中,谁因机器故障停止生产多少小时;
②当t等于多少时,甲、乙所生产的零件个数相等;
(2)谁在哪一段时间内的生产速度最快?求该段时间内,他每小时生产零件的个数.
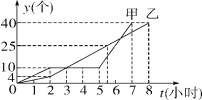
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,BD![]() AD,延长AD至点E,使D是AE的中点,连接BE和CE,BE与CD交于点F.
AD,延长AD至点E,使D是AE的中点,连接BE和CE,BE与CD交于点F.
(1)求证:四边形BDEC是矩形;
(2)若AB=6,AD=3,求矩形BDEC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com