练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知平行四边形ABCD中，BDAD，延长AD至点E，使D是AE的中点，连接BE和CE，BE与CD交于点F.

    （1）求证：四边形BDEC是矩形；

    （2）若AB=6，AD=3，求矩形BDEC的面积.

    【答案】（1）见解析；（2）9.

    【解析】

    （1）先证明四边形BCED为平行四边形，再证明∠BDE=90°即可；

    （2）由勾股定理得CE的长，再根据矩形的面积计算方法求解即可.

    （1）证明：∵D为AE中点

    ∴DE=AD

    ∵平行四边形ABCD

    ∴BC//AD

    ∴BC=AD

    ∴BC=DE

    ∴BC//DE

    ∴四边形BCED为平行四边形

    ∵BD⊥AE

    ∴∠BDE=90°

    ∴平行四边形BCED为矩形.

    （2）∵AD=3，

    ∴DE=3

    ∵AB=6，

    ∴CD=6，

    在Rt△CDE中，CE==

    面积为=.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

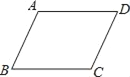
    【题目】如图，已知ABCD．

    （1）用直尺和圆规在BC边上取一点E，使AB=AE，连结AE；（保留作图痕迹，不写作法）

    （2）在（1）的前提下，求证：AE=CD；∠EAD=∠D；

    （3）若点E为BC的中点，连接BD，交AE于F，直接写出EF：FA的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列关于几何画图的语句，正确的是（ ）

    A.延长射线AB到点C，使BC=2AB

    B.点P在线段AB上，点Q在直线AB的反向延长线上

    C.将射线OA绕点O旋转，当终止位置OB与起始位置OA成一条直线时形成平角

    D.已知线段，若在同一直线上作线段AB=, BC=，则线段AC=

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB=90°，AC=4，BC=3，D是边AC的中点，CE⊥BD交AB于点E．

    （1）求tan∠ACE的值；

    （2）求AE：EB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

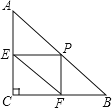
    【题目】如图，在Rt△ABC中，∠C=90°，AC=3，BC=4，P为AB边上（不与A、B重合的一动点，过点P分别作PE⊥AC于点E，PF⊥BC于点F，则线段EF的最小值是（ ）

    A. 2B. 3C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】1883年，德国数学家格奥尔格·康托尔引入位于一条线段上的一些点的集合，它的做法如下：

    取一条长度为1的线段，将它三等分，去掉中间一段，余下两条线段，达到第1阶段；将剩下的两条线段再分别三等分，各去掉中间一段，余下四条线段，达到第2阶段；再将剩四条线段，分别三等分，分别去掉中间一段，余下八条线段，达到第3阶段：…；这样的操作一直继续下去，在不断分割舍弃过程中，所形成的线段数目越来越多，把这种分形，称作康托尔点集，如图是康托尔点集的最初几个阶段，当达到第5个阶段时，余下的线段的长度之和为________；当达到第个阶段时（为正整数），余下的线段的长度之和为________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列代数式书写规范的是（　　）

    A. a÷3B. a8C. 5aD.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：a是最大的负整数，b是最小的正整数，且c＝a+b，请回答下列问题：

    （1）请直接写出a，b，c的值：a＝　 　；b＝　 　；c＝　 　；

    （2）a，b，c在数轴上所对应的点分别为A，B，C，请在如图的数轴上表示出A，B，C三点；

    （3）在（2）的情况下．点A，B，C开始在数轴上运动，若点A，点C以每秒1个单位的速度向左运动，同时，点B以每秒5个单位长度的速度向右运动，假设t秒钟过后，若点B与点C之间的距离表示为BC，点A与点B之间的距离表示为AB，请问：AB﹣BC的值是否随着时间的变化而改变？若变化，请说明理由；若不变，请求出AB﹣BC的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

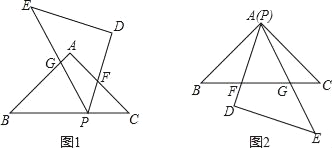
    【题目】如图，△ABC、△DEP是两个全等的等腰直角三角形，∠BAC=∠PDE=90°．

    （1）若将△DEP的顶点P放在BC上（如图1），PD、PE分别与AC、AB相交于点F、G．求证：△PBG∽△FCP；

    （2）若使△DEP的顶点P与顶点A重合（如图2），PD、PE与BC相交于点F、G．试问△PBG与△FCP还相似吗？为什么？

    查看答案和解析>>

    同步练习册答案