
����Ŀ��1883�꣬�¹���ѧ�Ҹ�¶��������ж�����λ��һ���߶��ϵ�һЩ��ļ��ϣ������������£�
ȡһ������Ϊ1���߶Σ��������ȷ֣�ȥ���м�һ�Σ����������߶Σ��ﵽ��1�Σ���ʣ�µ������߶��ٷֱ����ȷ֣���ȥ���м�һ�Σ����������߶Σ��ﵽ��2�Σ��ٽ�ʣ�����߶Σ��ֱ����ȷ֣��ֱ�ȥ���м�һ�Σ����°����߶Σ��ﵽ��3�Σ����������IJ���һֱ������ȥ���ڲ��Ϸָ����������У����γɵ��߶���ĿԽ��Խ�࣬�����ַ��Σ��������ж��㼯����ͼ�ǿ��ж��㼯����������Σ����ﵽ��5����ʱ�����µ��߶εij���֮��Ϊ________�����ﵽ��![]() ����ʱ��
����ʱ��![]() Ϊ�������������µ��߶εij���֮��Ϊ________.
Ϊ�������������µ��߶εij���֮��Ϊ________.


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͬѧ�ڼ���![]() ʱ������
ʱ������![]() ���������ˡ�
���������ˡ�![]() �����ó��Ľ����
����������![]() ��
��
(1)���������������ȷ�����
(2)��̽��������ĸ![]() ��
��![]() ����ʲô��ϵʱ��(1)�еĽ������ĸ
����ʲô��ϵʱ��(1)�еĽ������ĸ![]() ��ȡֵ�أ�
��ȡֵ�أ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ϵxOy�У�һ�κ���y����![]() x+5��ͼ��l1�ֱ���x��y�ύ��A��B���㣬������������ͼ��l2��l1���ڵ�C��m��3����
x+5��ͼ��l1�ֱ���x��y�ύ��A��B���㣬������������ͼ��l2��l1���ڵ�C��m��3����
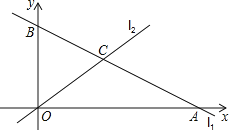
��1����m��ֵ��l2�Ľ���ʽ��
��2����S��AOC��S��BOC��ֵ��
��3��һ�κ���y��kx+1��ͼ��Ϊl3����11��l2��l3����Χ�������Σ�ֱ��д��k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
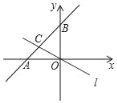
����Ŀ����ͼ����ֱ֪��y��x+4��x�ᡢy�ύ��A��B���㣬ֱ��l����ԭ�㣬���߶�AB���ڵ�C��������AOB�������Ϊ2��3�����֣���ֱ��l�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ƽ���ı���ABCD�У�BD![]() AD���ӳ�AD����E��ʹD��AE���е㣬����BE��CE��BE��CD���ڵ�F.
AD���ӳ�AD����E��ʹD��AE���е㣬����BE��CE��BE��CD���ڵ�F.
��1����֤���ı���BDEC�Ǿ��Σ�
��2����AB=6��AD=3�������BDEC�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
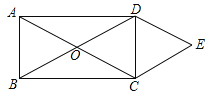
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��![]() ��
��![]() ����
����![]() ��
��![]() �����ı���OCED�����Ϊ___.
�����ı���OCED�����Ϊ___.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼOΪֱ��AB��һ�㣬��AOC��50����ODƽ�֡�AOC����DOE��90����

��1�����BOD�Ķ�����
��2�����ж�OE�Ƿ�ƽ�֡�BOC����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ı���ABCD���ĸ�����ֱ��ں���![]() ��
��![]()
![]() ��ͼ���ϣ��Խ���
��ͼ���ϣ��Խ���![]() �ᣬ��
�ᣬ��![]() �ڵ�
�ڵ�![]() .��֪��B�ĺ�����Ϊ4.
.��֪��B�ĺ�����Ϊ4.

��1����![]() ��
��![]() ʱ��
ʱ��
������P��������Ϊ2�����ı���ABCD�������
������P��BD���е㣬���ж��ı���ABCD����״����˵�����ɣ�
��2�����ı���ABCDΪ������ʱ��ֱ��д��m��n֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������1���෴���DZ�����������������2�������������С�ڱ���������3������ֵ�������෴�������Ǹ�������4��������������������1����5����![]() ����a=b����6��û�������������������ĸ�����.������ȷ�ĸ����� ��
����a=b����6��û�������������������ĸ�����.������ȷ�ĸ����� ��
A. 0 B. 1 C. 2 D. 3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com