
【题目】如图,在平面直角坐标系中,四边形ABCD的四个顶点分别在函数![]() 与
与![]()
![]() 的图象上,对角线
的图象上,对角线![]() 轴,且
轴,且![]() 于点
于点![]() .已知点B的横坐标为4.
.已知点B的横坐标为4.

(1)当![]() ,
,![]() 时,
时,
①若点P的纵坐标为2,求四边形ABCD的面积.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)当四边形ABCD为正方形时,直接写出m、n之间的数量关系.
【答案】(1)①![]() ;②四边形ABCD是菱形,见解析;(2)
;②四边形ABCD是菱形,见解析;(2)![]() .
.
【解析】
(1)①先确定出点A,B,C,D坐标,再利用面积的求法即可得出结论;
②先确定出点D坐标,进而确定出点P坐标,进而求出PA,PC,即可得出结论;
(2)先确定出B(4,![]() ),D(4,
),D(4,![]() ),进而求出点P的坐标,再求出A,C坐标,最后用AC=BD,即可得出结论.
),进而求出点P的坐标,再求出A,C坐标,最后用AC=BD,即可得出结论.
解:(1)①![]() ,
,![]() ,
,![]() ,
,![]() .
.
∵点B的横坐标为4,![]() .
.![]() .
.
![]() 轴,
轴,![]() ,点P的纵坐标为2,
,点P的纵坐标为2,
∴![]() ,
,![]() .
.![]() .
.
∴![]() ;
;
②四边形ABCD是菱形.
理由:![]() ,点P是线段BD的中点,
,点P是线段BD的中点,
![]() .
.
![]() 轴,
轴,![]() ,
,
![]()
∴![]() .
.![]() .
.
![]() ,∴四边形ABCD为平行四边形.
,∴四边形ABCD为平行四边形.
![]() ,∴四边形ABCD是菱形.
,∴四边形ABCD是菱形.
(2)![]() .
.
理由:当四边形ABCD是正方形,记AC,BD的交点为P,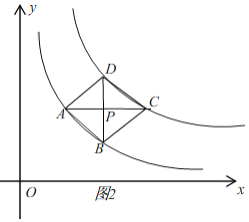
∴BD=AC
当x=4时,y=![]() =
=![]() , y=
, y=![]() =
=![]() ,
,
∴B(4,![]() ),D(4,
),D(4,![]() ),
),
∴P(4,![]() ),
),
∴A(![]() ,
, ![]() ),C(
),C(![]() ,
,![]() )
)
∵AC=BD,
∴![]() -
-![]() =
=![]() -
-![]() ,
,
∴m+n=32
故答案为:(1)①![]() ;②四边形ABCD是菱形,见解析;(2)
;②四边形ABCD是菱形,见解析;(2)![]() .
.


科目:初中数学 来源: 题型:
【题目】张先生今年7月份第一个星期的星期五以每股(份)25元的价格买进某种金融理财产品共2000股(买入时免收手续费),该理财产品在第二个星期的五个交易日中,每股的涨跌情况如下表(表格中数据表示比前一交易日涨或跌多少元) (单位:元):
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌额 |
|
|
|
|
|
(1)写出第二个星期每日每股理财产品的收盘价(即每日最后时刻的成交价);
(2)已知理财产品卖出时,交易所需收取千分之三的手续费,如果张先生在第二个星期的星期五交易结束前将全部产品卖出,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1883年,德国数学家格奥尔格·康托尔引入位于一条线段上的一些点的集合,它的做法如下:
取一条长度为1的线段,将它三等分,去掉中间一段,余下两条线段,达到第1阶段;将剩下的两条线段再分别三等分,各去掉中间一段,余下四条线段,达到第2阶段;再将剩四条线段,分别三等分,分别去掉中间一段,余下八条线段,达到第3阶段:…;这样的操作一直继续下去,在不断分割舍弃过程中,所形成的线段数目越来越多,把这种分形,称作康托尔点集,如图是康托尔点集的最初几个阶段,当达到第5个阶段时,余下的线段的长度之和为________;当达到第![]() 个阶段时(
个阶段时(![]() 为正整数),余下的线段的长度之和为________.
为正整数),余下的线段的长度之和为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
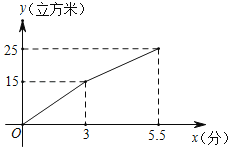
【题目】某种水泥储存罐的容量为25立方米,它有一个输入口和一个输出口.从某时刻开始,只打开输入口,匀速向储存罐内注入水泥,3分钟后,再打开输出口,匀速向运输车输出水泥,又经过2.5分钟储存罐注满,关闭输入口,保持原来的输出速度继续向运输车输出水泥,当输出的水泥总量达到8立方米时,关闭输出口.储存罐内的水泥量y(立方米)与时间x(分)之间的部分函数图象如图所示.
(1)求每分钟向储存罐内注入的水泥量.
(2)当3≤x≤5.5时,求y与x之间的函数关系式.
(3)储存罐每分钟向运输车输出的水泥量是 立方米,从打开输入口到关闭输出口共用的时间为 分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:a是最大的负整数,b是最小的正整数,且c=a+b,请回答下列问题:
![]()
(1)请直接写出a,b,c的值:a= ;b= ;c= ;
(2)a,b,c在数轴上所对应的点分别为A,B,C,请在如图的数轴上表示出A,B,C三点;
(3)在(2)的情况下.点A,B,C开始在数轴上运动,若点A,点C以每秒1个单位的速度向左运动,同时,点B以每秒5个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,请问:AB﹣BC的值是否随着时间的变化而改变?若变化,请说明理由;若不变,请求出AB﹣BC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数的图象经过点A(2,1),B(﹣1,﹣3).
(1)求此一次函数的解析式;
(2)求此一次函数的图象与x轴、y轴的交点坐标;
(3)求此一次函数的图象与两坐标轴所围成的三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC与△A′B′C′关于点P位似,且顶点都在格点上.
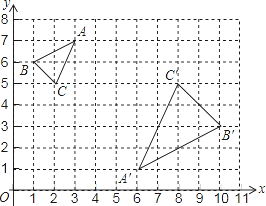
(1)在图上找出位似中心P的位置,并直接写出点P的坐标是;
(2)写出△ABC与△A′B′C′的面积比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店从厂家以21元的价格购进一批商品,该商品可以自行定价,若每件商品售价为![]() 元,则可卖出(350-10
元,则可卖出(350-10![]() )件,但物价局限定每件商品加价不能超过进价的20%,商店计划要赚400元,需要卖出多少件商品?每件商品应售多少元?
)件,但物价局限定每件商品加价不能超过进价的20%,商店计划要赚400元,需要卖出多少件商品?每件商品应售多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
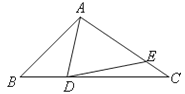
【题目】如图,在△ABC中,∠B=45°,在BC边上取一点D,使CD=CA,点E在AC上,连接ED,若∠AED=45°,且CE=1,BD=2,则AD的长是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com