
【题目】如图,在△ABC中,∠ACB=90°,AC=4,BC=3,D是边AC的中点,CE⊥BD交AB于点E.
(1)求tan∠ACE的值;
(2)求AE:EB.

【答案】(1)![]() (2)8:9
(2)8:9
【解析】试题分析:(1)根据同角的余角相等可证得: ∠ACE=∠CBD,因为点D是AC的中点,所以CD=2,所以tan∠ACE=tan∠CBD=![]() ,(2) 过A作AC的垂线交CE的延长线于P,
,(2) 过A作AC的垂线交CE的延长线于P,
在△CAP中,CA=4,∠CAP=90°,所以tan∠ACP=![]() ,所以AP=
,所以AP=![]() ,又因为∠ACB=90°,
,又因为∠ACB=90°,
∠CAP=90°,可证得BC∥AP, 所以AE:EB=AP:BC=8:9.
试题解析:(1)因为∠ACB=90°,CE⊥BD,
所以∠ACE=∠CBD,
在△BCD中,BC=3,CD=![]() AC=2,∠BCD=90°,
AC=2,∠BCD=90°,
tan∠CBD=![]() ,
,
即tan∠ACE=![]() .
.
(2)过A作AC的垂线交CE的延长线于P,
则在△CAP中,CA=4,∠CAP=90°,tan∠ACP=![]() ,
,
得AP=![]() ,
,
又∠ACB=90°,∠CAP=90°,得BC∥AP,
得AE:EB=AP:BC=8:9.


科目:初中数学 来源: 题型:
【题目】小颖在一张纸上画一条数轴,并在数轴上标出![]() 、
、![]() 、
、![]() 三个点,点
三个点,点![]() 表示的数是
表示的数是![]() ,点
,点![]() 在原点的右边且与点
在原点的右边且与点![]() 相距
相距![]() 个单位长度.
个单位长度.
(![]() )点
)点![]() 表示的数是__________.
表示的数是__________.
(![]() )将这张纸对折,此时点
)将这张纸对折,此时点![]() 与表示
与表示![]() 的点刚好重合,折痕与数轴交于点
的点刚好重合,折痕与数轴交于点![]() ,求点
,求点![]() 表示的数.
表示的数.
(![]() )若点
)若点![]() 到点
到点![]() 和点
和点![]() 的距离之和为
的距离之和为![]() ,求点
,求点![]() 所表示的数.
所表示的数.
(![]() )点
)点![]() 和点
和点![]() 同时从初始位置沿数轴向左运动,它们的速度分别是每秒
同时从初始位置沿数轴向左运动,它们的速度分别是每秒![]() 个单位长度和每秒
个单位长度和每秒![]() 个单位长度,运动时间是
个单位长度,运动时间是![]() 秒.是否存在
秒.是否存在![]() 的值,使
的值,使![]() 秒后点
秒后点![]() 到原点的距离与点
到原点的距离与点![]() 到原点的距离相等?若存在,请求出
到原点的距离相等?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,EG、EM、FM分别平分∠AEF,∠BEF,∠EFD,则图中与∠DFM相等的角(不含它本身)的个数为( ).

A. 7B. 6C. 5D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对称轴为直线x=1的抛物线y=ax2+bx+8过点(﹣2,0).
(1)求抛物线的表达式,并写出其顶点坐标;
(2)现将此抛物线沿y轴方向平移若干个单位,所得抛物线的顶点为D,与y轴的交点为B,与x轴负半轴交于点A,过B作x轴的平行线交所得抛物线于点C,若AC∥BD,试求平移后所得抛物线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图a是一个长为2m、宽为2n的长方形,沿图中实现用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.
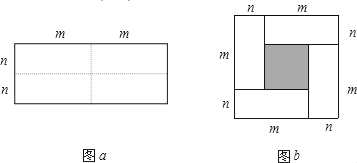
(1)图b中,大正方形的边长是 .阴影部分小正方形的边长是 ;
(2)观察图b,写出(m+n)2,(m﹣n)2,mn之间的一个等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五个城市的国际标准时间(单位:时)在数轴上表示如图所示,我市2015年初中毕业学业检测与高中阶段学校招生考试于2015年6月16日上午9时开始,此时应是( )
![]()
A. 纽约时间2015年6月16日晚上22时
B. 多伦多时间2015年6月15日晚上21时
C. 伦敦时间2015年6月16日凌晨1时
D. 汉城时间2015年6月16日上午8时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A与点B重合,折痕为DE,则S△BCE:S△BDE等于( )
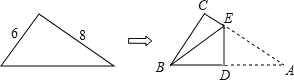
A.2:5 B.14:25 C.16:25 D.4:21
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com