
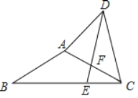
【题目】已知:在△ABC中,AB=AC=6,∠B=30°,E为BC上一点,BE=2EC,DE=DC,∠ADC=60°,则AD的长_____.
【答案】2![]()
【解析】
过A点做AG⊥BC,连接AE,可得△BAE为RT△,且∠AEB=60![]() ,∠AEC=120
,∠AEC=120![]() ,AE=CE,四边形DAEC共圆,可得∠ADE=∠CDE=
,AE=CE,四边形DAEC共圆,可得∠ADE=∠CDE=![]() ∠ADC=60°=30
∠ADC=60°=30![]() ,过点A做AO⊥CD与O点,可得△OAC为等腰直角三角形,可得OA的长,进而求出AD的长.
,过点A做AO⊥CD与O点,可得△OAC为等腰直角三角形,可得OA的长,进而求出AD的长.
解:如图: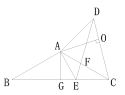
过A点做AG⊥BC,连接AE,![]() AB=AC
AB=AC
![]() G为BC的中点,在RT△ABG中,AB=AC=6,∠B=30°
G为BC的中点,在RT△ABG中,AB=AC=6,∠B=30°
![]() ∠ACB=30°,AG=
∠ACB=30°,AG=![]() =3,BG=CG=
=3,BG=CG=![]() ,
,
![]() BC=2BG=
BC=2BG=![]() ,
,
![]() 又BE=2EC,可得BE=
又BE=2EC,可得BE=![]() ,CE=
,CE=![]() ,
,![]() GE=
GE=![]()
在RT△AGE中,AE=![]() =
=![]() =
=![]() ,
,
![]() AE=CE=
AE=CE=![]() ,
,
在△BAE中,AB=6,BE=![]() ,AE=
,AE=![]() ,
,
可得![]()
![]() △BAE为RT△,∠BAE=90
△BAE为RT△,∠BAE=90![]() ,
,
![]() ∠B=30
∠B=30![]() ,
,
![]() ∠AEB=60
∠AEB=60![]() , ∠AEC=120
, ∠AEC=120![]() ,
,
在四边形DAEC中,∠ADC=60°,∠AEC=120![]() ,
,
![]() ∠ADC+∠AEC=180°,
∠ADC+∠AEC=180°,
![]() 四边形DAEC共圆,
四边形DAEC共圆,
![]() AE=CE=
AE=CE=![]()
![]() ∠ADE=∠CDE=
∠ADE=∠CDE=![]() ∠ADC=60°=30
∠ADC=60°=30![]() ,
,
过点A做AO⊥CD与O点,
在△DCE中,∠CDE=30![]() ,DE=DC
,DE=DC
![]() ∠DCE=
∠DCE=![]() =75
=75![]() ,
,![]() ∠ACB=30
∠ACB=30![]()
![]() ∠OCA=45
∠OCA=45![]() ,△OAC为等腰直角三角形
,△OAC为等腰直角三角形
在RT△OAC中,AC=6,∠OCA=45![]() ,
,![]() AO= AC
AO= AC![]() =
=![]() ,
,
在RT△AOD中, AO=![]() ,∠ADO=60
,∠ADO=60![]() ,可得AD=
,可得AD=![]() =
=![]() .
.
故答案:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
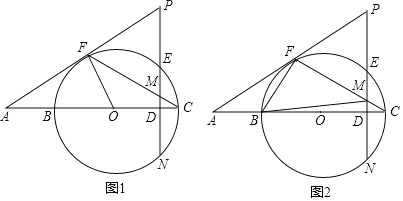
【题目】如图1,D是⊙O的直径BC上的一点,过D作DE⊥BC交⊙O于E、N,F是⊙O上的一点,过F的直线分别与CB、DE的延长线相交于A、P,连结CF交PD于M,∠C=![]() ∠P.
∠P.
(1)求证:PA是⊙O的切线;
(2)若∠A=30°,⊙O的半径为4,DM=1,求PM的长;
(3)如图2,在(2)的条件下,连结BF、BM;在线段DN上有一点H,并且以H、D、C为顶点的三角形与△BFM相似,求DH的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
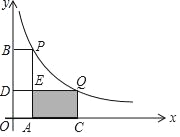
【题目】如图,在平面直角坐标系中,点P(1,4)、Q(m,n)在函数y=![]() (k>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A、B;过点Q分别作x轴、y轴的垂线,垂足为点C、D,QD交PA于点E,随着m的增大,四边形ACQE的面积( )
(k>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A、B;过点Q分别作x轴、y轴的垂线,垂足为点C、D,QD交PA于点E,随着m的增大,四边形ACQE的面积( )
A. 增大 B. 减小
C. 先减小后增大 D. 先增大后减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他各项费用80元.
销售单价x(元) | 3.5 | 5.5 |
销售量y(袋) | 280 | 120 |
(1)请直接写出y与x之间的函数关系式;
(2)如果每天获得160元的利润,销售单价为多少元?
(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的关系式;
(2)求△AOC的面积;
(3)求不等式kx+b-![]() <0的解集(直接写出答案).
<0的解集(直接写出答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知点A是双曲线y=kx-1(k>0)上的一个动点,连AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=mx-1(m<0)上运动,则m与k的关系是( )

A. m= -kB. m=![]() kC. m= -2kD. m= -3k
kC. m= -2kD. m= -3k
查看答案和解析>>
科目:初中数学 来源: 题型:
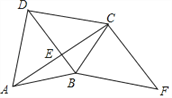
【题目】如图,四边形ABCD的对角线AC⊥BD于点E,AB=BC,F为四边形ABCD外一点,且∠FCA=90°,∠CBF=∠DCB.
(1)求证:四边形DBFC是平行四边形;
(2)如果BC平分∠DBF,∠CDB=45°,BD=2,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
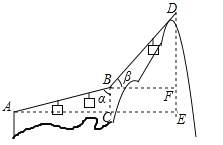
【题目】(2017安徽省)如图,游客在点A处做缆车出发,沿A﹣B﹣D的路线可至山顶D处,假设AB和BD都是直线段,且AB=BD=600m,α=75°,β=45°,求DE的长.
(参考数据:sin75°≈0.97,cos75°≈0.26,![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】社区利用一块矩形空地建了一个小型的惠民停车场,其布局如图所示.已知停车场的长为52米,宽为28米,阴影部分设计为停车位,要铺花砖,其余部分是等宽的通道.已知铺花砖的面积为640平方米.
(1)求通道的宽是多少米?
(2)该停车场共有车位64个,据调查分析,当每个车位的月租金为200元时,可全部租出;当每个车位的月租金每上涨10元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为14400元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com