
【题目】社区利用一块矩形空地建了一个小型的惠民停车场,其布局如图所示.已知停车场的长为52米,宽为28米,阴影部分设计为停车位,要铺花砖,其余部分是等宽的通道.已知铺花砖的面积为640平方米.
(1)求通道的宽是多少米?
(2)该停车场共有车位64个,据调查分析,当每个车位的月租金为200元时,可全部租出;当每个车位的月租金每上涨10元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为14400元?

【答案】(1)6;(2)40或400
【解析】
(1)设通道的宽x米,由图中所示可得通道面积为2×28x+2(52-2x)x,根据铺花砖的面积+通道面积=总面积列方程即可得答案;(2)设每个车位的月租金上涨a元,则少租出![]() 个车位,根据月租金收入为14400元列方程求出a值即可.
个车位,根据月租金收入为14400元列方程求出a值即可.
(1)设通道的宽x米,根据题意得:2×28x+2(52-2x)x+640=52×28,
整理得:x2-40x+204=0,
解得:x1=6,x2=34(不符合题意,舍去).
答:通道的宽是6米.
(2)设每个车位的月租金上涨a元,则少租出![]() 个车位,
个车位,
根据题意得:(200+a)(64-![]() )=14400,
)=14400,
整理得:a2-440a+16000=0,
解得:a1=40,a2=400.
答:每个车位的月租金上涨40元或400元时,停车场的月租金收入为14400元.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】已知x=﹣3是关于x的方程(k+3)x+2=3x﹣2k的解.
(1)求k的值;
(2)在(1)的条件下,已知线段AB=6cm,点C是直线AB上一点,且BC=kAC,若点D是AC的中点,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数y=kx+b的图象与y轴交于点B(0,1),与反比例函数y=![]() 的图象交于点A(3,﹣2).
的图象交于点A(3,﹣2).
(1)求反比例函数的表达式和一次函数表达式;
(2)若点C是y轴上一点,且BC=BA,直接写出点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某班数学兴趣小组利用数学活动课时间测量位于山顶的电视塔AB的高度,已知山的坡度为30°,山高857.5尺,组员从山脚D处沿山坡向着电视塔方向前进1620尺到达E点,在点E处测得电视塔顶端A的仰角为60°,求电视塔AB的高度.
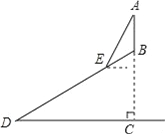
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分12分)在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过A(-3,0)、B(4,0)两点,且与y轴交于点C,点D在x轴的负半轴上,且BD=BC,有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时另一个动点Q从点C出发,沿线段CA以某一速度向点A移动.
经过A(-3,0)、B(4,0)两点,且与y轴交于点C,点D在x轴的负半轴上,且BD=BC,有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时另一个动点Q从点C出发,沿线段CA以某一速度向点A移动.
(1)求该抛物线的解析式;
(2)若经过t秒的移动,线段PQ被CD垂直平分,求此时t的值;
(3)该抛物线的对称轴上是否存在一点M,使MQ+MA的值最小?若存在,求出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图(1),![]() ,
,![]() ,
,![]() ,
,![]() 四点分别在四边形
四点分别在四边形![]() 的四条边上,若四边形
的四条边上,若四边形![]() 为菱形,我们称菱形
为菱形,我们称菱形![]() 为四边形
为四边形![]() 的内接菱形.
的内接菱形.
动手操作:

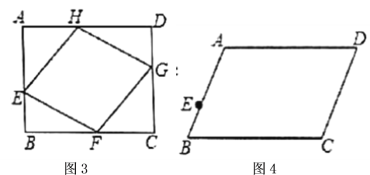
(1)如图2,网格中的每个小四边形都为正方形,每个小四边形的顶点叫做格点,由![]() 个小正方形组成一个大正方形
个小正方形组成一个大正方形![]() ,点
,点![]() 、
、![]() 在格点上,请在图(2)中画出四边形
在格点上,请在图(2)中画出四边形![]() 的内接菱形
的内接菱形![]() ;
;
特例探索:
(2)如图3,矩形![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上且
上且![]() ,四边形
,四边形![]() 是矩形
是矩形![]() 的内接菱形,求
的内接菱形,求![]() 的长度;
的长度;
拓展应用:
(3)如图4,平行四边形![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上且
上且![]() ,
,
①请你在图4中画出平行四边形![]() 的内接菱形
的内接菱形![]() ,点
,点![]() 在边
在边![]() 上;
上;
②在①的条件下,当![]() 的长最短时,
的长最短时,![]() 的长为__________
的长为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是AD边上的一点,AF⊥BE于F,CG⊥BE于G.
(1)若∠FAE=20°,求∠DCG的度数;
(2)猜想:AF,FG,CG三者之间的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 的边
的边![]() 上有一动点
上有一动点![]() ,从距离
,从距离![]() 点
点![]() 的点
的点![]() 处出发,沿线段
处出发,沿线段![]() 、射线
、射线![]() 运动,速度为
运动,速度为![]() ;动点
;动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 运动,速度为
运动,速度为![]() ;
;![]() 、
、![]() 同时出发,同时射线
同时出发,同时射线![]() 绕着点
绕着点![]() 从
从![]() 上以每秒5°的速度顺时针旋转,设运动时间是
上以每秒5°的速度顺时针旋转,设运动时间是![]() .
.
(1)当点![]() 在
在![]() 上运动时,
上运动时,![]()
![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 为何值时,
为何值时,![]() ?此时射线
?此时射线![]() 是
是![]() 的角平分线吗?如果是请说明理由.
的角平分线吗?如果是请说明理由.
(3)在射线![]() 上是否存在
上是否存在![]() 、
、![]() 相距
相距![]() ?若存在,请求出t的值并求出此时
?若存在,请求出t的值并求出此时![]() 的度数;若不存在,请说明理由.
的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(2,3)和点B(0,2),点A在反比例函数y= ![]() 的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为________.
的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为________.
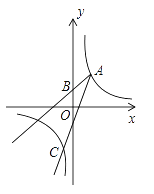
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com