
����Ŀ����ͼ����֪![]() ��
��![]() �ı�
�ı�![]() ����һ����
����һ����![]() ���Ӿ���
���Ӿ���![]() ��
��![]() �ĵ�
�ĵ�![]() �����������߶�
�����������߶�![]() ������
������![]() �˶����ٶ�Ϊ
�˶����ٶ�Ϊ![]() ������
������![]() �ӵ�
�ӵ�![]() ������������
������������![]() �˶����ٶ�Ϊ
�˶����ٶ�Ϊ![]() ��
��![]() ��
��![]() ͬʱ������ͬʱ����
ͬʱ������ͬʱ����![]() ���ŵ�
���ŵ�![]() ��
��![]() ����ÿ��5�����ٶ�˳ʱ����ת�����˶�ʱ����
����ÿ��5�����ٶ�˳ʱ����ת�����˶�ʱ����![]() ��
��
��1������![]() ��
��![]() ���˶�ʱ��
���˶�ʱ��![]()
![]() ���ú�
���ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2������![]() ���߶�
���߶�![]() ���˶�ʱ��
���˶�ʱ��![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ����ʱ����
����ʱ����![]() ��
��![]() �Ľ�ƽ�������������˵�����ɣ�
�Ľ�ƽ�������������˵�����ɣ�
��3��������![]() ���Ƿ����
���Ƿ����![]() ��
��![]() ���
���![]() �������ڣ������t��ֵ�������ʱ
�������ڣ������t��ֵ�������ʱ![]() �Ķ������������ڣ���˵�����ɣ�
�Ķ������������ڣ���˵�����ɣ�

���𰸡���1����18-2t������2��6���ǣ����ɼ���⣻��3�����ڣ�t=16����BOC=20���t=20����BOC=40�㣮
��������
��1����������ȷ����PM=2t���Ӷ��������ɵó����ۣ�
��2���������ȸ���OP=OQ�����������t=6�����������AOC=30�㣬���ɵó����ۣ�
��3�����������P��Q����ǰ���2cm��������2cm�������������������⣬���ɵó����ۣ�
�⣺��1������P��MO���˶�ʱ�����˶�֪��PM=2t��
��OM=18cm��
��PO=OM-PM=��18-2t��cm��
�ʴ�Ϊ����18-2t����
��2���ɣ�1��֪��OP=18-2t��
��OP=OQʱ������18-2t=t��
��t=6
��t=6ʱ����ʹOP=OQ��
������OC���ŵ�O��OA����ÿ��5����ٶ�˳ʱ����ת��
���AOC=5���6=30�㣬
�ߡ�AOB=60�㣬
���BOC=��AOB-��AOC=30��=��AOC��
������OC�ǡ�AOB�Ľ�ƽ���ߣ�
��3������������
��P��Q����ǰ���2cmʱ��
OQ-OP=2
��t-��2t-18��=2
��������̣���t=16��
���AOC=5���16=80��
���BOC=80��-60��=20�㣬
��P��Q���������2cmʱ��OP-OQ=2
�ࣨ2t-18��-t=2
�ⷽ�̵�t=20��
���AOC=5���20=100��
���BOC=100��-60��=40�㣬
�ۺ�����t=16����BOC=20���t=20����BOC=40�㣮


 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ϵ�![]() ����Ӧ�����ֱ�Ϊ
����Ӧ�����ֱ�Ϊ![]() ���Ҷ���Ϊ0����
���Ҷ���Ϊ0����![]() ���߶�
���߶�![]() ���е㣬��
���е㣬��![]() ����ԭ��
����ԭ��![]() ��λ�ã� ��
��λ�ã� ��
![]()
A.���߶�![]() ��B.���߶�
��B.���߶�![]() ���ӳ�����
���ӳ�����
C.���߶�![]() ��D.���߶�
��D.���߶�![]() ���ӳ�����
���ӳ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������һ����οյؽ���һ��С�͵Ļ���ͣ�������䲼����ͼ��ʾ.��֪ͣ�����ij�Ϊ52�ף���Ϊ28�ף���Ӱ�������Ϊͣ��λ��Ҫ�̻�ש�����ಿ���ǵȿ���ͨ��.��֪�̻�ש�����Ϊ640ƽ����.
��1����ͨ���Ŀ��Ƕ����ף�
��2����ͣ�������г�λ64�����ݵ����������ÿ����λ�������Ϊ200Ԫʱ����ȫ���������ÿ����λ�������ÿ����10Ԫ���ͻ������1����λ.��ÿ����λ����������Ƕ���Ԫʱ��ͣ���������������Ϊ14400Ԫ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�ֶ�������n�ġ�C���㡱���ٵ�nΪ����ʱ�����Ϊ3n��1���ڵ�nΪż��ʱ�����Ϊ![]() ������k��ʹ
������k��ʹ![]() Ϊ�������������������������ظ����У����磬n��66ʱ���䡰C���㡱����
Ϊ�������������������������ظ����У����磬n��66ʱ���䡰C���㡱����
![]()
��n��26�����2019�Ρ�C���㡱�Ľ����
A. 40 B. 5 C. 4 D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
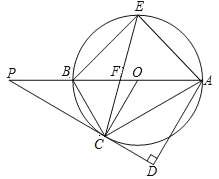
����Ŀ��������![]() �У�
��![]() ����
����![]() Ϊ
Ϊ![]() �ߵ��е㣬��
�ߵ��е㣬��![]() ���
���![]() ����
����![]() �Գƣ�����
�Գƣ�����![]() ��
��![]() ��
��![]() �����н��ۣ���
�����н��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() ��������ȷ���ǣ� ��
��������ȷ���ǣ� ��
A. �٢�B. �٢ڢ�C. �٢ڢ�D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��A�ְ���Ƴ�2��C��ģ�ߺ�1��D��ģ�ߣ���1��B�ְ���Ƴ�1��C��ģ�ߺ�3��D��ģ�ߣ�����A��B�ְ干100�飬��ȫ���ӹ���C��D��ģ�ߣ�
��1����B�ְ��������A�ְ����������������10�飬��A��B�ְ���ж��ٿ飿
��2��������C��D��ģ�ߵ�����ֱ�Ϊ80Ԫ/�顢100Ԫ/�飬��ȫ���۳���
�ٵ�A�ְ�����Ϊ25��ʱ����ô�����Ƴ�C��ģ�� ����D��ģ�� ����
�ڵ�C��D��ģ��ȫ���۳����õ�����Ϊ34400Ԫ����A�ְ��ж��ٿ飿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ɷ��֣�
��������
��1����M��ʾ������2����N��ʾ������8�����߶�MN���е�P��ʾ����Ϊ______��
��2����M��ʾ�����ǩ�3����N��ʾ������7�����߶�MN���е�P��ʾ����Ϊ_____�����֣���M��ʾ������a����N��ʾ������b�����߶�MN���е�P��ʾ����Ϊ______��
ֱ�����ã�
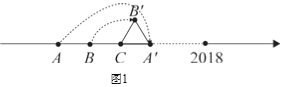
�����ᰴ��ͼ1��ʾ���ӵ�A��ʼ�۳�һ���ȱ�������A'B'C�����A��ʾ����Ϊx��3����B��ʾ����Ϊ2x+1��C��ʾ����Ϊx��1����xֵΪ_____��������A'B'C��ͼ��λ�����ҹ���������2018��Ӧ�ĵ㽫���A'B'C�Ķ���_______�غϣ�
���Ǩ�ƣ�
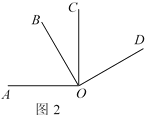
��ͼ2��OA��OC��OB��OD����COD��60����������OA��O����ÿ��15�����ٶ�˳ʱ����ת������OB��O����ÿ��10�����ٶ�˳ʱ����ת������OC��O����ÿ��5�����ٶ���ʱ����ת������ͬʱ��ת����һ������������OD�غ�ʱ����������ͬʱֹͣ�˶���
��������OC������OB����ʱ����AOB�Ķ�����
���˶�����ʱ������OA�ǡ�BOC��ƽ���ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
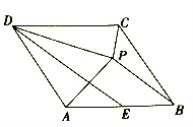
����Ŀ����ͼ��ʾ��AB �ǡ�O ��ֱ����P Ϊ AB �ӳ����ϵ�һ�㣬PC �С�O �ڵ� C��AD��PC�� ����Ϊ D���� CE ƽ�֡�ACB���� AB �ڵ� F������ AE��
��1����֤��PC=PF��
��2���� tan��ABC=![]() ��AE=5
��AE=5![]() �����߶� PC �ij���
�����߶� PC �ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���ֱ��![]() �У�
��![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() �۵���ʹ��
�۵���ʹ��![]() ���
���![]() �غϣ�
�غϣ�![]() Ϊ�ۺۣ���
Ϊ�ۺۣ���![]() ��ֵ�ǣ� ��
��ֵ�ǣ� ��
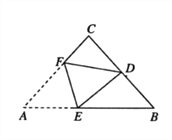
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com