【题目】在菱形
中，
，点
为
边的中点，点
与点
关于
对称，连接
、
、
，下列结论：①
；②
；③
；④
，其中正确的是（ ）
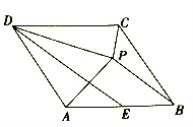
A. ①②B. ①②③C. ①②④D. ①②③④
口算题卡北京妇女儿童出版社系列答案科目：初中数学 来源： 题型：
【题目】姐姐和妹妹按计划周末去距家18km的电影院看电影，由于妹妹需要去书店买课外书，姐姐也要完成妈妈布置的家务任务，所以姐姐让妹妹骑公共自行车先出发，然后自己坐公交赶到电影院与妹妹聚齐．如图是她们所走的路程y km与所用时间x min的函数图象， 观察此函数图象得出有关信息：
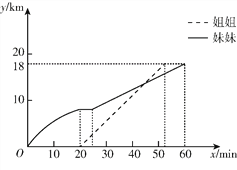
①妹妹比姐姐早出发20min；②妹妹买书用了10 min；③妹妹的平均速度为18km/h；④姐姐大约用了52 min到达电影院．其中正确的个数为
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（本题满分12分）在平面直角坐标系
中，抛物线
经过A（－3,0）、B（4,0）两点，且与y轴交于点C，点D在x轴的负半轴上，且BD＝BC，有一动点P从点A出发，沿线段AB以每秒1个单位长度的速度向点B移动，同时另一个动点Q从点C出发，沿线段CA以某一速度向点A移动.
（1）求该抛物线的解析式；
（2）若经过t秒的移动，线段PQ被CD垂直平分，求此时t的值；
（3）该抛物线的对称轴上是否存在一点M，使MQ＋MA的值最小？若存在，求出点M的坐标；若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在正方形ABCD中，点E是AD边上的一点，AF⊥BE于F，CG⊥BE于G．
（1）若∠FAE=20°，求∠DCG的度数；
（2）猜想：AF，FG，CG三者之间的数量关系，并证明你的猜想．
查看答案和解析>>
科目：初中数学 来源： 题型：
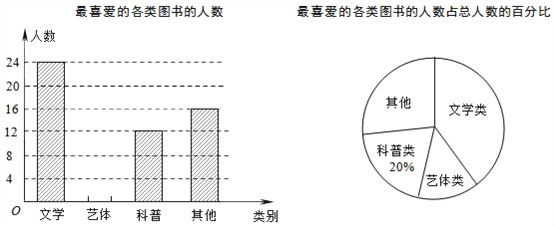
【题目】某出版社为了了解在校大学生最喜爱的图书类别（图书分为文学类、艺体类、科普类、其他等四类），在广州某大学进行随机调查，并将调查结果绘制成如下两幅不完整的统计图（如图所示），请你结合图中的信息解答下列问题：
（1）求被调查的学生人数；
（2）补全条形统计图；
（3）已知该校有12000名学生，估计全校最喜爱文学类图书的学生有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知
，
的边
上有一动点
，从距离
点
的点
处出发，沿线段
、射线
运动，速度为
；动点
从点出发，沿射线运动，速度为
；、同时出发，同时射线
绕着点从上以每秒5°的速度顺时针旋转，设运动时间是
．
（1）当点在上运动时，
（用含
的代数式表示）；
（2）当点在线段上运动时，为何值时，
？此时射线是的角平分线吗？如果是请说明理由．
（3）在射线上是否存在、相距
？若存在，请求出t的值并求出此时
的度数；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知线段
，点
为线段
上的一个动点，点
分别是
和
的中点.
(1)若点恰好是中点，则
;
(2)若
,求
的长;
(3)试利用“字母代替数”的方法，说明不论取何值(不超过
)，的长不变.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是一个汉字“互”字，其中，AB∥CD，∠1=∠2，∠MGH=∠MEF.
求证：∠MEF=∠GHN.
证明：∵ AB∥CD（已知）
∴∠1=∠3（ ）
又∵∠1=∠2（已知）
∴∠2=∠3（ ）
∴ME∥HN （ ）
∴∠MGH=∠ ( )( )
又∵∠MGH=∠MEF (已知)
∴∠MEF=∠GHN（ ）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
