
【题目】定义一种对正整数n的“C运算”:①当n为奇数时,结果为3n+1;②当n为偶数时,结果为![]() (其中k是使
(其中k是使![]() 为奇数的正整数),并且运算重复进行.例如,n=66时,其“C运算”如下
为奇数的正整数),并且运算重复进行.例如,n=66时,其“C运算”如下
![]()
若n=26,则第2019次“C运算”的结果是
A. 40 B. 5 C. 4 D. 1
科目:初中数学 来源: 题型:
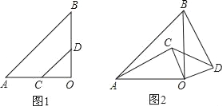
【题目】如图1、图2,△AOB,△COD均是等腰直角三角形,∠AOB=∠COD=90°,
(1)在图1中,AC与BD相等吗?请说明理由;
(2)若△COD绕点O顺时针旋转一定角度后,到达图2的位置,请问AC与BD还相等吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
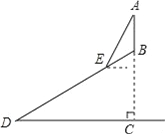
【题目】如图,某班数学兴趣小组利用数学活动课时间测量位于山顶的电视塔AB的高度,已知山的坡度为30°,山高857.5尺,组员从山脚D处沿山坡向着电视塔方向前进1620尺到达E点,在点E处测得电视塔顶端A的仰角为60°,求电视塔AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图(1),![]() ,
,![]() ,
,![]() ,
,![]() 四点分别在四边形
四点分别在四边形![]() 的四条边上,若四边形
的四条边上,若四边形![]() 为菱形,我们称菱形
为菱形,我们称菱形![]() 为四边形
为四边形![]() 的内接菱形.
的内接菱形.
动手操作:

(1)如图2,网格中的每个小四边形都为正方形,每个小四边形的顶点叫做格点,由![]() 个小正方形组成一个大正方形
个小正方形组成一个大正方形![]() ,点
,点![]() 、
、![]() 在格点上,请在图(2)中画出四边形
在格点上,请在图(2)中画出四边形![]() 的内接菱形
的内接菱形![]() ;
;
特例探索:
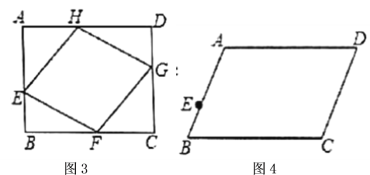
(2)如图3,矩形![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上且
上且![]() ,四边形
,四边形![]() 是矩形
是矩形![]() 的内接菱形,求
的内接菱形,求![]() 的长度;
的长度;
拓展应用:
(3)如图4,平行四边形![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上且
上且![]() ,
,
①请你在图4中画出平行四边形![]() 的内接菱形
的内接菱形![]() ,点
,点![]() 在边
在边![]() 上;
上;
②在①的条件下,当![]() 的长最短时,
的长最短时,![]() 的长为__________
的长为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是AD边上的一点,AF⊥BE于F,CG⊥BE于G.
(1)若∠FAE=20°,求∠DCG的度数;
(2)猜想:AF,FG,CG三者之间的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是两张不同类型火车的车票:(“D×××次”表示动车,“G×××次”表示高铁):
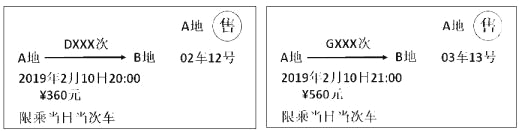
(1)根据车票中的信息填空:两车行驶方向 ,出发时刻 (填“相同”或“不同”);
(2)已知该动车和高铁的平均速度分别为200km/h,300km/h,如果两车均按车票信息准时出发,且同时到达终点,求A,B两地之间的距离;
(3)在(2)的条件下,请求出在什么时刻两车相距100km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 的边
的边![]() 上有一动点
上有一动点![]() ,从距离
,从距离![]() 点
点![]() 的点
的点![]() 处出发,沿线段
处出发,沿线段![]() 、射线
、射线![]() 运动,速度为
运动,速度为![]() ;动点
;动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 运动,速度为
运动,速度为![]() ;
;![]() 、
、![]() 同时出发,同时射线
同时出发,同时射线![]() 绕着点
绕着点![]() 从
从![]() 上以每秒5°的速度顺时针旋转,设运动时间是
上以每秒5°的速度顺时针旋转,设运动时间是![]() .
.
(1)当点![]() 在
在![]() 上运动时,
上运动时,![]()
![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 为何值时,
为何值时,![]() ?此时射线
?此时射线![]() 是
是![]() 的角平分线吗?如果是请说明理由.
的角平分线吗?如果是请说明理由.
(3)在射线![]() 上是否存在
上是否存在![]() 、
、![]() 相距
相距![]() ?若存在,请求出t的值并求出此时
?若存在,请求出t的值并求出此时![]() 的度数;若不存在,请说明理由.
的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台湾是中国领土不可分割的一部分,两岸在政治、经济、文化等领域交流越来越深,在北京故宫博物院成立90周年院庆时,两岸故宫同根同源,合作举办了多项纪念活动.据统计,北京故宫博物院与台北故宫博物院现共有藏品约245万件,其中台北故宫博物院藏品数量比北京故宫博物院藏品数量的![]() 还少25万件,求北京故宫博物院约有多少万件藏品?
还少25万件,求北京故宫博物院约有多少万件藏品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宁波至绍兴城际列车已于2019年7月10日运营,这是国内首条利用既有铁路改造开行的跨市域城际铁路.其中余姚至绍兴的成人票价12元/人,学生票价6元/人.余姚某校801班师生共计50人坐城际列车去绍兴秋游.
(1)设有![]() 名老师,求801班师生从余姚到绍兴的城际列车总费用
名老师,求801班师生从余姚到绍兴的城际列车总费用![]() 关于
关于![]() 的函数表达式.
的函数表达式.
(2)若从余姚到绍兴的城际列车总费用![]() 不超过330元,问至少有几名学生?
不超过330元,问至少有几名学生?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com