
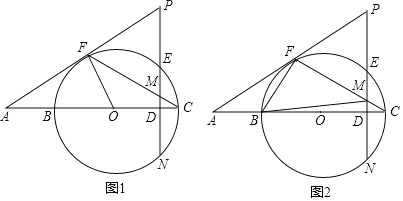
【题目】如图1,D是⊙O的直径BC上的一点,过D作DE⊥BC交⊙O于E、N,F是⊙O上的一点,过F的直线分别与CB、DE的延长线相交于A、P,连结CF交PD于M,∠C=![]() ∠P.
∠P.
(1)求证:PA是⊙O的切线;
(2)若∠A=30°,⊙O的半径为4,DM=1,求PM的长;
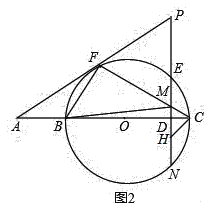
(3)如图2,在(2)的条件下,连结BF、BM;在线段DN上有一点H,并且以H、D、C为顶点的三角形与△BFM相似,求DH的长度.
【答案】(1)证明见解析;(2)PM=4![]() ﹣2;(3)满足条件的DH的值为
﹣2;(3)满足条件的DH的值为![]() 或
或![]() .
.
【解析】
(1)如图1中,作PH⊥FM于H.想办法证明∠PFH=∠PMH,∠C=∠OFC,再根据等角的余角相等即可解决问题;
(2)解直角三角形求出AD,PD即可解决问题;
(3)分两种情形①当△CDH∽△BFM时,![]() .
.
②当△CDH∽△MFB时,![]() ,分别构建方程即可解决问题;
,分别构建方程即可解决问题;
(1)证明:如图1中,作PH⊥FM于H.

∵PD⊥AC,∴∠PHM=∠CDM=90°,∵∠PMH=∠DMC,∴∠C=∠MPH,
∵∠C=![]() ∠FPM,∴∠HPF=∠HPM,
∠FPM,∴∠HPF=∠HPM,
∵∠HFP+∠HPF=90°,∠HMP+∠HPM=90°,∴∠PFH=∠PMH,
∵OF=OC,∴∠C=∠OFC,
∵∠C+∠CMD=∠C+∠PMF=∠C+∠PFH=90°,
∴∠OFC+∠PFC=90°,∴∠OFP=90°,
∴直线PA是⊙O的切线.
(2)解:如图1中,∵∠A=30°,∠AFO=90°,∴∠AOF=60°,
∵∠AOF=∠OFC+∠OCF,∠OFC=∠OCF,∴∠C=30°,
∵⊙O的半径为4,DM=1,
∴OA=2OF=8,CD=![]() DM=
DM=![]() ,
,
∴OD=OC﹣CD=4﹣![]() ,
,
∴AD=OA+OD=8+4﹣![]() =12﹣
=12﹣![]() ,
,
在Rt△ADP中,
DP=ADtan30°=(12﹣![]() )×
)×![]() =4
=4![]() ﹣1,
﹣1,
∴PM=PD﹣DM=4 ![]() ﹣2.
﹣2.
(3)如图2中,
由(2)可知:BF=![]() BC=4,FM=
BC=4,FM=![]() BF=4
BF=4![]() ,CM=2DM=2,CD=
,CM=2DM=2,CD=![]() ,
,
∴FM=FC﹣CM=4![]() ﹣2,
﹣2,
①当△CDH∽△BFM时,![]() ,
,
∴ ![]() ,∴DH=
,∴DH=![]()
②当△CDH∽△MFB时,![]() ,
,
∴![]() ,∴DH=
,∴DH=![]() ,
,
∵DN=![]() ,
,
∴DH<DN,符合题意,
综上所述,满足条件的DH的值为![]() 或
或![]() .
.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
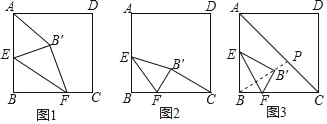
【题目】正方形ABCD的边长是10,点E是AB的中点,动点F在边BC上,且不与点B、C重合,将△EBF沿EF折叠,得到△EB′F.
(1)如图1,连接AB′.
①若△AEB′为等边三角形,则∠BEF等于多少度.
②在运动过程中,线段AB′与EF有何位置关系?请证明你的结论.
(2)如图2,连接CB′,求△CB′F周长的最小值.
(3)如图3,连接并延长BB′,交AC于点P,当BB′=6时,求PB′的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
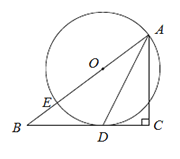
【题目】已知:如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC边相切于点D,连结AD.
(1)求证:AD是∠BAC的平分线;
(2)若AC=3,BC=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(发现)x4﹣5x2+4=0是一个一元四次方程.
(探索)根据该方程的特点,通常用“换元法”解方程:
设x2=y,那么x4=y2,于是原方程可变为 .
解得:y1=1,y2= .
当y=1时,x2=1,∴x=±1;
当y= 时,x2= ,∴x= ;
原方程有4个根,分别是 .
(应用)仿照上面的解题过程,求解方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在茶节期间,某茶商订购了甲种茶叶90吨,乙种茶叶80吨,准备用A、B两种型号的货车共20辆运往外地.已知A型货车每辆运费为0.4万元,B型货车每辆运费为0.6万元.(13分)
(1)设A型货车安排x辆,总运费为y万元,写出y与x的函数关系式;
(2)若一辆A型货车可装甲种茶叶6吨,乙种茶叶2吨;一辆B型货车可装甲种茶叶3吨,乙种茶叶7吨.按此要求安排A、B两种型号货车一次性运完这批茶叶,共有哪几种运输方案?
(3)说明哪种方案运费最少?最少运费是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
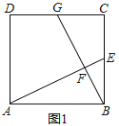
小明遇到这样一个问题:如图1,在正方形ABCD中,点E是边BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若AB=6,AF=4EF,求CG的值与∠AFB的度数.
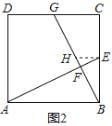
他的做法是:过点E作EH∥AB交BG于点H,得到△BAF∽△HEF(如图2).
(1)CG等于多少,∠AFB等于多少度;
参考小明思考问题的方法,解决下列问题;
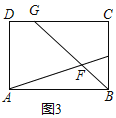
(2)如图3,在矩形ABCD中,点E是边BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若AF=3EF,求![]() 的值;
的值;
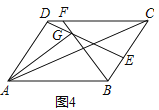
(3)如图4,在平行四边形ABCD中,E、F分别是边BC、CD上的点,BF和DE相交于点G,且AB=kAD,∠DAG=∠BAC,求出![]() 的值(用含k的式子表示)
的值(用含k的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
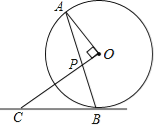
【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为![]() ,OP=1,求BC的长.
,OP=1,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com