
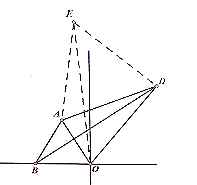
【题目】如图,在平面直角坐标系中,已知![]() 是等边三角形,边
是等边三角形,边![]() 上有一点
上有一点![]() ,且
,且![]() 、
、![]() 两点之间的距离为
两点之间的距离为![]() .
.

(1)求![]() 的坐标(用含有
的坐标(用含有![]() 的式子表示);
的式子表示);
(2)如图(1),若点![]() 在线段
在线段![]() 上运动,点
上运动,点![]() 在
在![]() 轴的正半轴上运动.当
轴的正半轴上运动.当![]() 的值最小时,
的值最小时,![]() .
.
问:![]() 的面积是否为定值,若是,求其值;若不是,请说明理由.
的面积是否为定值,若是,求其值;若不是,请说明理由.
(3)如图(2),若在![]() 外还有一点
外还有一点![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)(m-6,0);(2)是定值为25![]() ,理由见解析(3)12
,理由见解析(3)12
【解析】
(1)根据![]() ,且
,且![]() 、
、![]() 两点之间的距离为
两点之间的距离为![]() ,即可写出
,即可写出![]() 的坐标;
的坐标;
(2)作出点E关于y轴的对称点E’,得到PE=PE’,E’为定点,P、F为动点,过E’作E’F⊥AB,交y轴于点P,此时PE+PF=E’F,E’F为点E’到AB的距离,为最小,若BF=7,△BFE’为直角三角形,根据∠B=60°得到BE’=14,EE’=8,OE=4,OB=10,即可求解△ABO的面积;
(3)将△ABD旋转60°到△AOE,得到OE=BD=15,△AED为等边三角形,得到DE=AD=9,∠ADE=60°,再得到∠EDO=90°,利用勾股定理即可求解.
(1)∵![]() ,且
,且![]() 、
、![]() 两点之间的距离为
两点之间的距离为![]() ,
,
∴![]() 的坐标为(m-6,0);
的坐标为(m-6,0);
(2)作出点E关于y轴的对称点E’,
∴PE=PE’,
∵E(m,0)
∴E’为定点,P、F为动点,过E’作E’F⊥AB,交y轴于点P,此时PE+PF=E’F,
E’F为点E’到AB的距离,为最小,
若BF=7,△BFE’为直角三角形,
∵∠B=60°∴∠BE’F=30°,
∴BE’=14,
∵BE=6
∴EE’=8,
∴OE=4,
则OB=10,
∴S△ABO=![]() =
=![]() =25
=25![]() ;
;

(3)将△ABD旋转60°到△AOE,
∴△ABD≌△AOE,
∴OE=BD=15,
∵AD=AE,∠EAD=60°,
∴△AED为等边三角形,得到DE=AD=9,∠ADE=60°,
∵![]()
∴∠EDO=∠ADE +∠ADO= 90°,
∴OD=![]()


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,将其绕点A逆时针旋转15°得到Rt△AB′C′,B′C′交AB于E,若图中阴影部分面积为![]() ,则B′E的长为__.
,则B′E的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图
如图![]() ,
,![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,在
,在![]() 上截取
上截取![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .求证:四边形
.求证:四边形![]() 是菱形;
是菱形;
![]() 如图
如图![]() ,
,![]() 中,
中,![]() 平分
平分![]() 的外角
的外角![]() 交
交![]() 的延长线于点
的延长线于点![]() ,在
,在![]() 的延长线上截取
的延长线上截取![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .四边形
.四边形![]() 还是菱形吗?如果是,请证明;如果不是,请说明理由.
还是菱形吗?如果是,请证明;如果不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
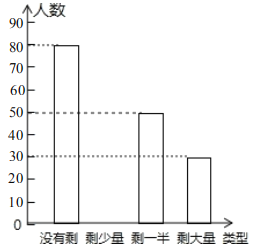
【题目】为更好地践行社会主义核心价值观,让同学们珍惜粮食,学会感恩,校学生会积极倡导“光盘小行动”,某天午餐后学生会干部随机调查了部分同学就餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
(1)这次被调查的同学共有 名;
(2)补全条形统计图;
(3)计算在扇形统计图中剩大量饭菜所对应扇形圆心的度数;
(4)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人用一餐,据此估算,全校![]() 名学生一餐浪费的食物可供多少人食用一餐?
名学生一餐浪费的食物可供多少人食用一餐?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4张相同的卡片上分别写有数字2,3,4,5将卡片的背面向上,洗匀后从中任意抽取1 张,将卡片上的数字作为被减数;一只不透明的袋子中装有标号2,3,4的3个小球,这些球除标号外都相同,搅匀后从中任意摸出一个球,将摸到的球的标号作为减数.
(1)用树状图或列表的方法求这两个数的差为0的概率;
(2)如果游戏规则规定:当抽到的这两个数的差为非负数时,则甲获胜;否则,乙获胜,你认为这样的规则公平吗?如果不公平,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】形如:![]() 的函数叫二次函数,它的图象是一条抛物线.类比一元一次方程的解可以看成两条直线的交点的横坐标;则一元二次方程
的函数叫二次函数,它的图象是一条抛物线.类比一元一次方程的解可以看成两条直线的交点的横坐标;则一元二次方程![]() 的解可以看成抛物线
的解可以看成抛物线![]() 与直线
与直线![]() (
(![]() 轴)的交点的横坐标;也可以看成是抛物线
轴)的交点的横坐标;也可以看成是抛物线![]() 与直线
与直线![]() ________的交点的横坐标;也可以看成是抛物线
________的交点的横坐标;也可以看成是抛物线![]() ________与直线
________与直线![]() 的交点的横坐标;
的交点的横坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组对关于![]() 的方程
的方程![]() 提出了下列问题.
提出了下列问题.
![]() 若使方程为一元二次方程,
若使方程为一元二次方程,![]() 是否存在?若存在,求出
是否存在?若存在,求出![]() 并解此方程.
并解此方程.
![]() 若使方程为一元一次方程,
若使方程为一元一次方程,![]() 是否存在?若存在,请求出.你能解决这个问题吗?
是否存在?若存在,请求出.你能解决这个问题吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com