
����Ŀ����ƽ��ֱ������ϵ�У���֪������y=x2+bx+c�Ķ���M������Ϊ����1����4��������x�ύ�ڵ�A����B����A�ڵ�B����ߣ�����y�ύ�ڵ�C��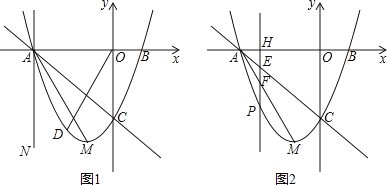
��1����գ�b= �� c= �� ֱ��AC�Ľ���ʽΪ
��2��ֱ��x=t��x���ཻ�ڵ�H��
�ٵ�t=��3ʱ�õ�ֱ��AN����ͼ1������DΪֱ��AC�·���������һ�㣬����COD=��MAN�������ʱ��D�����ꣻ
�ڵ���3��t����1ʱ����ͼ2����ֱ��x=t���߶�AC��AM�������߷ֱ��ཻ�ڵ�E��F��P����֤���߶�HE��EF��FP������ɵ��������Σ�����˵��������εǵ�����ֵΪ ![]() �����ʱt��ֵ��
�����ʱt��ֵ��
���𰸡�
��1��2����3��y=��x��3
��2��
�⣺�����D������Ϊ��m��m2+2m��3����
�ߡ�COD=��MAN��
��tan��COD=tan��MAN��
�� ![]() =
= ![]() ��
��
��ã�m=�� ![]() ��
��
�ߩ�3��m��0��
��m=�� ![]() ��
��
�ʵ�D������Ϊ���� ![]() ����2
����2 ![]() ����
����
����ֱ��AM�Ľ���ʽΪy=mx+n��
����A����3��0����M����1����4�����룬
�ã� ![]() ����ã�
����ã� ![]() ��
��
��ֱ��AM�Ľ���ʽΪ��y=��2x��6��
�ߵ�x=tʱ��HE=������t��3��=t+3��HF=������2t��6��=2t+6��HP=����t2+2t��3����
��HE=EF=HF��HE=t+3��FP=��t2��4t��3��
��HE+EF��FP=2��t+3��+t2+4t+3=��t+3��2��0��
��HE+EF��FP��
��HE+FP��EF��EF+FP��HE��
�൱��3��t����1ʱ���߶�HE��EF��FP������ɵ��������Σ�
������ã� ![]() =
= ![]() ����
���� ![]() =
= ![]() ��
��
�����ã�5t2+26t+33=0��
��ã�t1=��3��t2=�� ![]() ��
��
�ߩ�3��t����1��
��t=�� ![]() ��
��
���������⣺��1����������y=x2+bx+c�Ķ���M������Ϊ����1����4����
�� 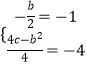 ����ã�
����ã� ![]() ��
��
�������߽���ʽΪ��y=x2+2x��3��
��y=0���ã�x2+2x��3=0����ã�x1=1��x2=��3��
��A����3��0����B��1��0����
��x=0����y=��3��
��C��0����3����
��ֱ��AC�Ľ���ʽΪ��y=kx+b��
��A����3��0����C��0����3�����룬
�ã� ![]() ����ã�
����ã� ![]() ��
��
��ֱ��AC�Ľ���ʽΪ��y=��x��3��
���Դ��ǣ�2����3��y=��x��3��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��a��b��cΪ������a��0��������A����1��0����B��5����6����C��6��0����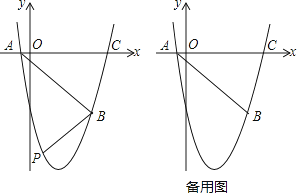
��1���������ߵĽ���ʽ��
��2����ͼ����ֱ��AB�·������������Ƿ���ڵ�Pʹ�ı���PACB�������������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��3������QΪ�����ߵĶԳ����ϵ�һ�����㣬��ָ����QABΪ���������εĵ�Qһ���м����������������ijһ����Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ղ����
�涨��a2��a��a��a3��a��a��a��an��a��a������a��n �� a��
(1)��2��3��2�� ��22��32�� ���㷢����2�� 3��2 ��ֵ�� 22��32 ��ֵ ��
(2)��2��3��3�� ��23��33�� ���㷢����2��3��3 ��ֵ�� 23��33 ��ֵ ��
�ɴ������ǿ��Բ�������a��b��2 a2��b2����a��b��3 a3��b3������a��b��n an��bn.
(3)����(2)����ۼ�������2��2018������![]() ��2019 ��ֵ��
��2019 ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������˵����![]() ��״��ͬ��ͼ����ȫ���Σ�
��״��ͬ��ͼ����ȫ���Σ�![]() ȫ���εĴ�С��ͬ����״Ҳ��ͬ��
ȫ���εĴ�С��ͬ����״Ҳ��ͬ��![]() ȫ�������ε������ȣ�
ȫ�������ε������ȣ�![]() �����ȵ�����������ȫ�ȣ�
�����ȵ�����������ȫ�ȣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ������ȷ��˵����
������ȷ��˵����![]() ����
����![]()
A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
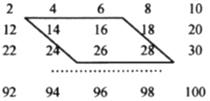
����Ŀ����ͼ��ʾ����������50��ż���ųɵ�.
(1)ͼ�п��ڵ�4������ʲô��ϵ?
(2)������ͼ��������һ������(1)�еĿ������е�һ����Ϊ![]() ����ô����������������ʾ?
����ô����������������ʾ?
(3)����ĸ����ĺ���172���ܷ������4����?
(4)����ĸ����ĺ���322���ܷ������4����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߶� AB=24������ P �� A ��������ÿ�� 2 ����λ���ٶ������� AB�˶����˶�ʱ��Ϊ t ����t>0����M Ϊ AP ���е�.
��1������ P ���߶� AB ���˶�ʱ��
�ٵ� t Ϊ����ʱ��PB=2AM������2BM-BP��ֵ.
��2���� P �� AB �ӳ������˶�ʱ��N Ϊ BP ���е���˵���߶� MN �ij��Ȳ������� �����ֵ.
��3���� P ����˶����������Ƿ���������� t ��ֵ��ʹ M��N��B �����е�һ���� ������������Ϊ�˵���߶ε��е�������������� t ��ֵ����û������˵���� ��.
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ���⣺
��һЩ��ͬ�ķ�����Ҫ��ˢ��һ�� 3��һ������ȥ��ˢ 8�����䣬��������� 50![]() ǽ��δ���ü�ˢ��ͬ��ʱ���� 5������������ˢ�� 10������֮�⣬����ˢ�������40
ǽ��δ���ü�ˢ��ͬ��ʱ���� 5������������ˢ�� 10������֮�⣬����ˢ�������40![]() ǽ�森��֪ÿ��ͬ����ļ���ÿ��Ĺ���Ч����ͬ��ÿ��һ�������ȶ�������ÿ���ˢ 10
ǽ�森��֪ÿ��ͬ����ļ���ÿ��Ĺ���Ч����ͬ��ÿ��һ�������ȶ�������ÿ���ˢ 10![]() ǽ�棬��ÿ��һ�������Ͷ�������ÿ���ˢ��ǽ����Ƕ���ƽ����?
ǽ�棬��ÿ��һ�������Ͷ�������ÿ���ˢ��ǽ����Ƕ���ƽ����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ij��ҵ������Ӧ���������·�չ���ĺ��٣��з���һ���²�Ʒ����֪�з����������ֲ�Ʒ�ijɱ�Ϊ30Ԫ/��������������y������������ۼ�x��Ԫ/�����ĺ�������ʽΪ��y= ![]() ��
��
��1������ҵ���۸ò�Ʒ��õ�������ΪW����Ԫ������ֱ��д��������W����Ԫ�������ۼ�x��Ԫ/�����ĺ�������ʽ��
��2�����ò�Ʒ���ۼ�x��Ԫ/����Ϊ����ʱ����ҵ���۸ò�Ʒ��õ��������������������Ƕ��٣�
��3������ҵ���۸ò�Ʒ������������750��Ԫ����ȷ���ò�Ʒ���ۼ�x��Ԫ/������ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ּƻ��Ѽ��ֻ���1240�ֺ����ֻ���880����һ�л�������ij�أ���֪���л�������A��B���ֲ�ͬ���Ļ������Ṳ40�ڣ�ʹ��A�ͳ���ÿ�ڷ���Ϊ6000Ԫ��ʹ��B�ͳ���ÿ�ڷ���Ϊ8000Ԫ��
��1������������������ܷ���Ϊ![]() ��Ԫ�����л�����A�ͳ���
��Ԫ�����л�����A�ͳ���![]() �ڣ���д��
�ڣ���д��![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2�����ÿ��A�ͳ�������װ���ֻ���35�ֺ����ֻ���15�֣�ÿ��B�ͳ�������װ���ֻ���25�ֺ����ֻ���35�֣�װ��ʱ����Ҫ����A��B���ֳ���Ľ�������ô�����ļ��ְ��ų���ķ�����
��3�������������У����ַ����˷���ʡ�������˷�Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com