
分析 (1)证明△>0即可;
(2)利用抛物线与x轴的交点问题,则x1、x2为方程mx2-8mx+16m-1=0的两根,利用根与系数的关系得到x1+x2=8,x1•x2=$\frac{16m-1}{m}$,再变形|x1-x2|=2得到(x1+x2)2-4x1•x2=4,所以82-4•$\frac{16m-1}{m}$=4,然后解出m即可得到抛物线解析式;
(3)先求出抛物线的对称轴为直线x=4,利用函数图象,由于抛物线开口向上,则只要当x=2,y≥0时,抛物线与线段CD有交点,于是得到4m-16m+16m-1≥0,然后解不等式即可.
解答 (1)证明:△=64m2-4m•(16m-1)
=4m,
∵m>0,
∴△>0,
∴抛物线总与x轴有两个不同的交点;
(2)根据题意,x1、x2为方程mx2-8mx+16m-1=0的两根,
∴x1+x2=-$\frac{-8m}{m}$=8,x1•x2=$\frac{16m-1}{m}$,
∵|x1-x2|=2,
∴(x1+x2)2-4x1•x2=4,
∴82-4•$\frac{16m-1}{m}$=4,
∴m=1,
∴抛物线的解析式为y=x2-8x+15;
(3)抛物线的对称轴为直线x=-$\frac{-8m}{2m}$=4,
∵抛物线开口向上,
∴当x=2,y≥0时,抛物线与线段CD有交点,
∴4m-16m+16m-1≥0,
∴m≥$\frac{1}{4}$.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了根与系数的关系.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
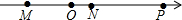 点M,N,P和原点O在数轴上的位置如图所示,点M,N,P对应的有理数为a,b,c(对应顺序暂不确定).如果ab<0,a+b>0,ac>bc,那么表示数b的点为( )
点M,N,P和原点O在数轴上的位置如图所示,点M,N,P对应的有理数为a,b,c(对应顺序暂不确定).如果ab<0,a+b>0,ac>bc,那么表示数b的点为( )| A. | 点M | B. | 点N | C. | 点P | D. | 点O |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| A | … | … | |||||
| B | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某蔬菜基地要把一批新鲜蔬菜运往外地,有两种运输方式可供选择,主要参看数据如下:
某蔬菜基地要把一批新鲜蔬菜运往外地,有两种运输方式可供选择,主要参看数据如下:| 运输方式 | 运输速度(km/h) | 装卸费用(元) | 途中综合费用(元/h) |
| 汽车 | m | 200 | 270 |
| 火车 | 100 | n | 240 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com