
 某蔬菜基地要把一批新鲜蔬菜运往外地,有两种运输方式可供选择,主要参看数据如下:
某蔬菜基地要把一批新鲜蔬菜运往外地,有两种运输方式可供选择,主要参看数据如下:| 运输方式 | 运输速度(km/h) | 装卸费用(元) | 途中综合费用(元/h) |
| 汽车 | m | 200 | 270 |
| 火车 | 100 | n | 240 |
分析 (1)根据“总费用=装卸费用+途中综合费用”这一等量关系求出m、n的值,利用待定系数法列方程组可求出函数关系式;
(2)节省的费用是汽车运输费用减去火车运输费用,结合运输路程的范围可知节省的最少费用.
解答 解:(1)由函数图象知,当运输路程x=100时,汽车、火车的运输总费用均为650元,根据题意得
$200+270×\frac{100}{m}=650,解得m=60$;
$n+240×\frac{100}{100}=650,解得n=410$;
设汽车运输的总费用y1与运输路程x间的函数关系式为:y1=k1x+b1,
∵当运输路程x=0km时,运输总费用即装卸费用为200元;
∴将x=0、y=200和x=100、y=650代入函数关系式得
$\left\{\begin{array}{l}{{b}_{1}=200}\\{100{k}_{1}+{b}_{1}=650}\end{array}\right.,解得\left\{\begin{array}{l}{{k}_{1}=4.5}\\{{b}_{1}=200}\end{array}\right.$;
∴汽车运输的总费用y1与运输路程x间的函数关系式为:y1=4.5x+200;
设火车运输的总费用y2与运输路程x间的函数关系式为:y2=k2x+b2;
将x=0、y=410和x=100、y=650代入函数关系式得
$\left\{\begin{array}{l}{{b}_{2}=410}\\{100{k}_{2}+{b}_{2}=650}\end{array}\right.,解得\left\{\begin{array}{l}{{k}_{2}=2.4}\\{{b}_{2}=410}\end{array}\right.$,
∴火车运输的总费用y2与运输路程x间的函数关系式为:y2=2.4x+410.
(2)∵汽车途中用时比火车的途中用时多用2小时以上(含2小时)
∴$\frac{x}{60}-\frac{x}{100}≥2,解得x≥300$;
记运用火车运输比用汽车运输节省W元,则
w=y1-y2
=4.5x+200-(2.4x+410)
=2.1x-210
∵W随x的增大而减小,且x≥300;
∴当x=300时,W取得最小值,最小值为410.
故此时运用火车运输比用汽车运输至少节省410元.
点评 本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题.注意利用一次函数求最值时,关键是应用一次函数的性质;即由函数y随x的变化,结合自变量的取值范围确定最值.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,平面内有公共端点的四条射线OA,OB,OC,OD,从射线OA开始按逆时针方向依次在射线上写出数字2,-4,6,-8,10,-12,….则第16个数应是-32;“-2016”在射线OD上.
如图,平面内有公共端点的四条射线OA,OB,OC,OD,从射线OA开始按逆时针方向依次在射线上写出数字2,-4,6,-8,10,-12,….则第16个数应是-32;“-2016”在射线OD上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在等腰Rt△ABC中,∠ABC=90°,O是AC的中点,P,Q分别在AB,BC上(P,Q与A,B,C都不重合),OP⊥OQ,OS⊥AQ交AB于S.下列结论:①BQ=BS;②PA=QB;③S是PB的中点;④$\frac{CQ}{PS}$的值为定值.其中正确结论的个数是( )
如图,在等腰Rt△ABC中,∠ABC=90°,O是AC的中点,P,Q分别在AB,BC上(P,Q与A,B,C都不重合),OP⊥OQ,OS⊥AQ交AB于S.下列结论:①BQ=BS;②PA=QB;③S是PB的中点;④$\frac{CQ}{PS}$的值为定值.其中正确结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
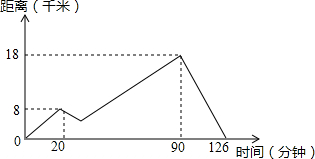 如图表示一条船从点A到河的上游点B往返的情形,从A点出发20分钟后,发动机坏了一段时间,船顺着河水倒着走了一段,之后发动机修好,继读前进到达,接着立即向点A返回.假设河水的流速、船行驶时在静水中的速度是不变的,这艘船在静水中的速度是多少?
如图表示一条船从点A到河的上游点B往返的情形,从A点出发20分钟后,发动机坏了一段时间,船顺着河水倒着走了一段,之后发动机修好,继读前进到达,接着立即向点A返回.假设河水的流速、船行驶时在静水中的速度是不变的,这艘船在静水中的速度是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com