
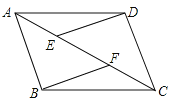
【题目】如图,在ABCD中,E、F为对角线AC上的两点,且AE=CF,连接DE、BF,
(1)写出图中所有的全等三角形;
(2)求证:DE∥BF.
【答案】(1)△ABC≌△CDA,△ABF≌△△CDE,△ADE≌△CBF;(2)证明见试题解析.
【解析】
试题分析:(1)根据平行四边形的性质得出AB=CD,AD=CB,AB∥CD,AD∥CB,进一步得到∠BAF=∠DCE,∠DAE=∠BCF,由SSS证明△ABC≌△CDA;由SAS证明△ABF≌△CDE;由SAS证明△ADE≌△CBF(SAS);
(2)由△ABF≌△△CDE,得出∠AFB=∠CED,即可证出DE∥BF.
试题解析:(1)△ABC≌△CDA,△ABF≌△△CDE,△ADE≌△CBF;理由如下:
∵四边形ABCD是平行四边形,∴AB=CD,AD=CB,AB∥CD,AD∥CB,∴∠BAF=∠DCE,∠DAE=∠BCF,在△ABC和△CDA中,∵AB=CD,CB=AD,AC=CA,∴△ABC≌△CDA(SSS);
∵AE=CF,∴AF=CE,在△ABF和△CDE中,∵AB=CD,∠BAF=∠DCE,AF=CE,∴△ABF≌△CDE(SAS);
在△ADE和△CBF中,∵AD=CB,∠DAE=∠BCF,AE=CF,∴△ADE≌△CBF(SAS).
(2)∵△ABF≌△△CDE,∴∠AFB=∠CED,∴DE∥BF.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD=![]() ,求
,求![]() 的值.
的值.
(3)(3分)在(2)的条件下,设⊙O的半径为3,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上.则细线的另一端所在位置的点的坐标是 . 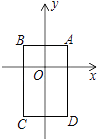
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC , D为边BC上一点,以AB、BD为邻边作平行四边形ABDE , 连接AD、EC . 若BD=CD , 求证:四边形ADCE是矩形.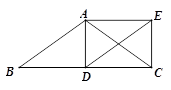
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是( )
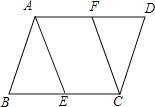
A. AF=CE B. AE=CF C. ∠BAE=∠FCD D. ∠BEA=∠FCE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品原价为200元,连续两次降价x%后,售价为148元.下面所列方程正确的是( )
A.200(1﹣x%)2=148B.200(1+x%)2=148
C.200(1﹣2x%)=148D.200(1﹣x2%)=148
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com