练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】绝对值不大于2的非负整数有_________．.绝对值小于100的所有整数的和是_____________ .

    【答案】 0,1,2 0

    【解析】试题解析：绝对值不大于2的非负整数有0，1，2；

    绝对值小于100的所有整数有：-99，-98，-97，┈97，98，99

    故：（-99）+（-98）+（-97）+┈+97+98+99=0.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下面去括号中错误的是 ( )

    A. a＋(b－c) ＝a＋b－c B. a－(b＋c－d)＝a－b－c－d

    C. m＋2(p－q)＝m＋2p－2q D. x－3(y＋z)＝x－3y－3z

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某厂生产A、B两种产品，其单价随市场变化而做相应调整，营销人员根据前三次单价变化的情况，绘制了如下统计表及不完整的折线图.

    并求得了A产品三次单价的平均数和方差：

    A=5.9；s2A=[（6-5.9）2＋（5.2-5.9）2＋（6.5-5.9）2]= .

    （1）补全图中B产品单价变化的折线图. B产品第三次的单价比上一次的单价降低了 %；

    （2）求B产品三次单价的方差，并比较哪种产品的单价波动小；

    （3）该厂决定第四次调价，A产品的单价仍为6.5元/件，B产品的单价比3元/件上调m%（m＞0），使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1，求m的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】实验室里，水平桌面上有甲、乙、丙三个相 同高度的圆柱形容器（容器足够高），底面半径之比为1:2:1，用两个相同的管子在10cm高度处连通（即管子底部离容器底10cm），现三个容器中，只有乙中有水，水位高4cm，如图所示．若每分钟同时向甲和丙注入相同量的水，开始注水1分钟，甲的水位上升3cm．则开始注入 分钟水量后，甲的水位比乙高1cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】当三角形中一个内角α是另一个内角β的两倍时，我们称此三角形为“特征三角形”，其中α称为“特征角”．如果一个“特征三角形”的“特征角”为100°，那么这个“特征三角形”的最小内角的度数为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在坐标系中放置一菱形OABC，已知∠ABC=60°，OA=1．先将菱形OABC沿x轴的正方向无滑动翻转，每次翻转60°，连续翻转2014次，点B的落点依次为B1，B2，B3，…，则B2014的坐标为 ．

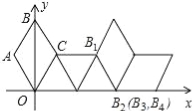
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】平面上，矩形ABCD与直径为QP的半圆K如图摆放，分别延长DA和QP交于点O，且∠DOQ＝60°，OQ＝OD＝3，OP＝2，OA＝AB＝1，让线段OD及矩形ABCD位置固定，将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转，设旋转角为α(0°≤α≤60°)．

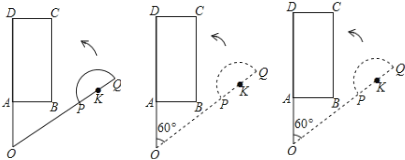
    发现：

    （1）当α＝0°，即初始位置时，点P 直线AB上(选填“在”或“不在”)．

    当α= 时，OQ经过点B；

    （2）在OQ旋转过程中，α= 时，点P，A间的距离最小？PA最小值为 ；

    （3）探究当半圆K与矩形ABCD的边相切时，求sinα的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCO的边OA、OC在坐标轴上，点B坐标为（6，6），将正方形ABCO绕点C逆时针旋转角度α（0°＜α＜90°），得到正方形CDEF，ED交线段AB于点G，ED的延长线交线段OA于点H，连CH、CG．

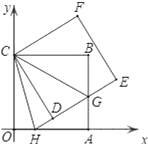
    （1）求证：△CBG≌△CDG；

    （2）求∠HCG的度数；并判断线段HG、OH、BG之间的数量关系，说明理由；

    （3）连结BD、DA、AE、EB得到四边形AEBD，在旋转过程中，四边形AEBD能否为矩形？如果能，请求出点H的坐标；如果不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将方程2x＋3＝3x＋2变形后，得2x－3x＝2－3，根据是(　　)

    A. 等式的基本性质1 B. 等式的基本性质2

    C. 合并同类项的法则 D. 以上均不对

    查看答案和解析>>

    同步练习册答案