
���� ��1������AB����֮��ľ���Ϊx�ף��������ֲ��з������ٶ���ȣ��г����̼�����⣻
��2�������A�ص�C��һ������ʱ��Ϊy���ӣ���������������������С��������904��·���������г����̼�����⣮
��� �⣺��1���践��ʱA��B���ؼ��·��Ϊx�ף�������ã�
$\frac{x+200}{25}$=$\frac{x}{25-2.5}$��
���x=1800��
��A��B���ؼ��·��Ϊ1800�ף�
��2����С����A�ص�B�ع�������y���ӣ�������ã�
25��6+5��10+[10+��y-30����1]��y-30��=904��
������y2-50y-104=0��
���y1=52��y2=-2����ȥ����
��С����A�ص�C�ع�����52���ӣ�
���� ������һԪһ�η��̵�Ӧ�ã�һԪ���η��̵�Ӧ�ã�����ؼ���Ҫ������Ŀ����˼��������Ŀ�������������ҳ����ʵĵ�����ϵ�г����̣�����⣮


 �ظ���ʦ�㲦ϵ�д�
�ظ���ʦ�㲦ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
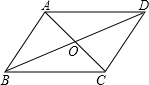 ��ͼ��AC��BD��ƽ���ı���ABCD�ĶԽ��ߣ�AC��BD���ڵ�O����AC=4��BD=5��BC=3�����BOC���ܳ��ǣ�������
��ͼ��AC��BD��ƽ���ı���ABCD�ĶԽ��ߣ�AC��BD���ڵ�O����AC=4��BD=5��BC=3�����BOC���ܳ��ǣ�������| A�� | 7.5 | B�� | 6 | C�� | 12 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\sqrt{��-6��^{2}}$=-6 | B�� | ��-$\sqrt{3}$��2=-3 | C�� | $\sqrt{��-16��^{2}}$=��16 | D�� | $\sqrt{{a}^{2}}$=a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -4 | B�� | 6 | C�� | 4 | D�� | -6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
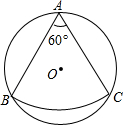 ��ͼ����һ��뾶��1m��Բ����Ƥ����O���ϼ���һ��Բ�Ľ�Ϊ60������Σ���A��B��C�ڡ�O�ϣ��������µ�����Χ��һ��Բ�������Բ�ĵ���Բ�İ뾶�ǣ�������
��ͼ����һ��뾶��1m��Բ����Ƥ����O���ϼ���һ��Բ�Ľ�Ϊ60������Σ���A��B��C�ڡ�O�ϣ��������µ�����Χ��һ��Բ�������Բ�ĵ���Բ�İ뾶�ǣ�������| A�� | $\frac{\sqrt{3}}{6}$m | B�� | $\frac{\sqrt{3}}{12}$m | C�� | $\frac{\sqrt{3}}{2}$m | D�� | 1m |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ����O��AB��AC���е�ֱ�Ϊ��E�͵�F��ֱ��EF��AC�ڵ�P����AB�ڵ�Q����ô��APQ��ʲô�����Σ���֤����Ľ��ۣ�
��ͼ��ʾ����O��AB��AC���е�ֱ�Ϊ��E�͵�F��ֱ��EF��AC�ڵ�P����AB�ڵ�Q����ô��APQ��ʲô�����Σ���֤����Ľ��ۣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
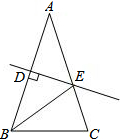 ��ͼ������������ABC���ܳ�Ϊ23���ױ�BC=5��AB�Ĵ�ֱƽ����DE��AB�ڵ�D����AC�ڵ�E�����BEC���ܳ�Ϊ14��
��ͼ������������ABC���ܳ�Ϊ23���ױ�BC=5��AB�Ĵ�ֱƽ����DE��AB�ڵ�D����AC�ڵ�E�����BEC���ܳ�Ϊ14���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | -2 | C�� | 4 | D�� | -8 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com