
| A. | 0 | B. | 1 | C. | -1 | D. | 2014 |
分析 设a为负整数,将x=a代入得:$\frac{{a}^{2}-1}{{a}^{2}+1}$,将x=-$\frac{1}{a}$代入得:$\frac{(-\frac{1}{a})^{2}-1}{(-\frac{1}{a})^{2}+1}$=$\frac{\frac{1-{a}^{2}}{{a}^{2}}}{\frac{{a}^{2}+1}{{a}^{2}}}$=$\frac{1-{a}^{2}}{{a}^{2}+1}$,故此可知当x互为负倒数时,两分式的和为0,然后求得分式的值即可.
解答 解:∵将x=a代入得:$\frac{{a}^{2}-1}{{a}^{2}+1}$,将x=-$\frac{1}{a}$代入得:$\frac{(-\frac{1}{a})^{2}-1}{(-\frac{1}{a})^{2}+1}$=$\frac{\frac{1-{a}^{2}}{{a}^{2}}}{\frac{{a}^{2}+1}{{a}^{2}}}$=$\frac{1-{a}^{2}}{{a}^{2}+1}$,
∴$\frac{{a}^{2}-1}{{a}^{2}+1}$+$\frac{1-{a}^{2}}{{a}^{2}+1}$=0,
故当x分别取2016、2015、2014…、2、1、1、$\frac{1}{2}$、$\frac{1}{3}$、…、$\frac{1}{2014}$、$\frac{1}{2015}$、$\frac{1}{2016}$时,得出分式$\frac{{x}^{2}-1}{{x}^{2}+1}$的值,再将所得结果相加,其和等于:0.
故选:A.
点评 本题主要考查的是分式的加减,发现当x的值互为负倒数时,两分式的和为0是解题的关键.


科目:初中数学 来源: 题型:填空题
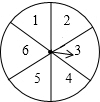 转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等.四位同学各自发表了下述见解:
转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等.四位同学各自发表了下述见解:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,弦CD⊥AB于H,E为AB延长线上一点,CE交⊙O于点F
如图,AB为⊙O的直径,弦CD⊥AB于H,E为AB延长线上一点,CE交⊙O于点F查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com