
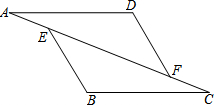
 如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,AD∥BC,AD=BC.求证:BE∥DF.
如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,AD∥BC,AD=BC.求证:BE∥DF.  品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | -1 | D. | 2014 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当a≠0时,分式$\frac{2}{a}$有意义 | B. | 当a=-3时,分式$\frac{a+3}{{{a^2}-9}}$有意义 | ||
| C. | 当$a=-\frac{1}{2}$时,分式$\frac{2a+1}{a}$的值为0 | D. | 当a=1时,分式$\frac{2a-1}{a}$的值为1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
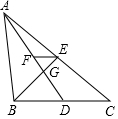 如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,则FG:AG是( )
如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,则FG:AG是( )| A. | 1:4 | B. | 1:3 | C. | 1:2 | D. | 2:3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
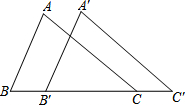 如图,在△ABC中,AB=8,BC=12,∠B=60°,将△ABC沿着射线BC的方向平移4个单位后,得到△A'B'C',连接AC,则△A'B'C的面积是( )
如图,在△ABC中,AB=8,BC=12,∠B=60°,将△ABC沿着射线BC的方向平移4个单位后,得到△A'B'C',连接AC,则△A'B'C的面积是( )| A. | 16 | B. | $4\sqrt{3}$ | C. | $16\sqrt{3}$ | D. | $32\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
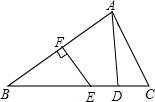 如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.
如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com