
分析 (1)根据待定系数法即可求得;
(2)分两种情况,根据平行四边形的性质分别讨论即可求得.
解答 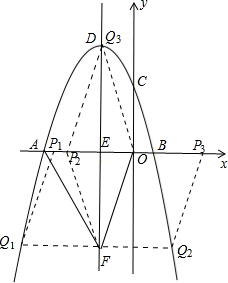 解:(1)据题意得$\left\{\begin{array}{l}9a-3b+3=0\\ a+b+3=0.\end{array}\right.解得\left\{\begin{array}{l}a=-1\\ b=-2.\end{array}\right.$
解:(1)据题意得$\left\{\begin{array}{l}9a-3b+3=0\\ a+b+3=0.\end{array}\right.解得\left\{\begin{array}{l}a=-1\\ b=-2.\end{array}\right.$
∴解析式为y=-x2-2x+3;
(2)∵y=-x2-2x+3=-(x+1)2+4,
∴顶点D(-1,4),
∴F(-1,-4),
若以点O、F、P、Q为顶点的平行四边形存在,则点Q(x,y)满足|y|=EF=4,
①当y=-4时,-x2-2x+3=-4,
解得,x=-1±2$\sqrt{2}$,
∴Q1(-1-2$\sqrt{2}$,-4),Q2(-1+2$\sqrt{2}$,-4),
∴P1(-2$\sqrt{2}$,0),P2(2$\sqrt{2}$,0),
②当y=4时,-x2-2x+3=4,
解得,x=-1
∴Q3(-1,4)
∴P3(-2,0),
综上所述,符合条件的点有三个即:P1(-2$\sqrt{2}$,0),P2(2$\sqrt{2}$,0),P3(-2,0).
点评 本题是二次函数的综合题,考查了待定系数法求解析式以及平行四边形的性质,根据题意求得Q的坐标是解题的关键.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源:2016-2017学年陕西省咸阳市七年级下学期第一次月考数学试卷(解析版) 题型:单选题
若A=(2+1)(22+1)(24+1)(28+1),则A的末位数字是( ).
A. 4 B. 5 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
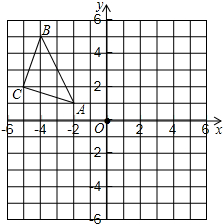 如图,△ABC在平面直角坐标系中,其中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).
如图,△ABC在平面直角坐标系中,其中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
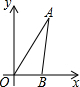 选做题:从甲乙两题中选作一题,如果两题都做,只以甲题计分
选做题:从甲乙两题中选作一题,如果两题都做,只以甲题计分查看答案和解析>>
科目:初中数学 来源: 题型:填空题
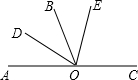 如图所示,若∠AOB与∠BOC是一对邻补角,OD平分∠AOB,OE在∠BOC内部,并且∠BOE=$\frac{1}{2}$∠COE,∠DOA=30°,则∠COE的度数是80°.
如图所示,若∠AOB与∠BOC是一对邻补角,OD平分∠AOB,OE在∠BOC内部,并且∠BOE=$\frac{1}{2}$∠COE,∠DOA=30°,则∠COE的度数是80°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
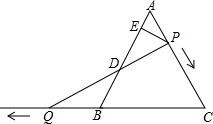 如图,已知△ABC是等腰三角形,且∠C=60°,AB=10,点P是AC边上一动点,由点A向点C运动(点P与点A、C不重合),Q是CB延长线上一点,与 点P同时以相同的速度由点B向CB延长线方向运动(点Q与点B不重合),过点P作PE⊥AB于点E,连结PQ交AB于点D.
如图,已知△ABC是等腰三角形,且∠C=60°,AB=10,点P是AC边上一动点,由点A向点C运动(点P与点A、C不重合),Q是CB延长线上一点,与 点P同时以相同的速度由点B向CB延长线方向运动(点Q与点B不重合),过点P作PE⊥AB于点E,连结PQ交AB于点D.查看答案和解析>>
科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:填空题
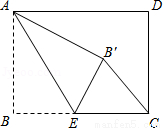
如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com