
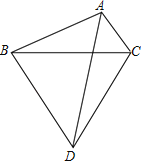
【题目】如图,在△ABC中,∠BAC=120°,以BC为边向外作等边△BCD.
(Ⅰ)∠ABD+∠ACD=_____.
(Ⅱ)∠BAD=_____.
(Ⅲ)若AB=3,AC=2,求AD的长.
【答案】(Ⅰ)180°;(Ⅱ)60°;(Ⅲ)AD=5.
【解析】
(Ⅰ)根据四边形内角和360°可求;
(Ⅱ)将△ACD绕点D逆时针旋转60°,得到△BED,证明A、B、E三点共线,所以△ADE是等边三角形,则∠BAD=60°;
(Ⅲ)根据BE=AC=2,则AE=AB+BE=3+2=5,则等边△ADE的边AD=5.
(Ⅰ)因为四边形内角和360°,
所以∠BAD+∠BDC+∠ABD+∠ACD=360°,
∴∠ABD+∠ACD=360°﹣120°﹣60°=180°.
故答案为180°;
(Ⅱ)将△ACD绕点D逆时针旋转60°,得到△BED(如图所示),
∵DC=BD,∠BDC=60°,
∴旋转后的三角形DC与BD重合.
又∠ABD+∠ACD=180°,
所以∠ABD+∠EBD=180°,
∴A、B、E三点共线.
所以△ADE是等边三角形,
∴∠BAD=60°.
故答案为60°;
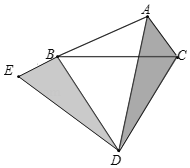
(Ⅲ)根据(Ⅱ)可知BE=AC=2,则AE=AB+BE=3+2=5.
所以AD=5.
故答案为180°,60°.


科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0),点B(3,0),交y轴于点C,给出下列结论:①a:b:c=﹣1:2:3;②对于任意实数m,一定有am2+bm+a≤0;③元二次方程cx2+bx+a=0的两根为﹣1和![]() ,其中正确的结论是( )
,其中正确的结论是( )
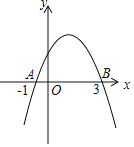
A.①②③B.①②C.①③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
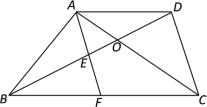
【题目】如图,在梯形ABCD中,AD//BC,AC与BD相交于点O,点E在线段OB上,AE的延长线与BC相交于点F,OD2 = OB·OE.
(1)求证:四边形AFCD是平行四边形;
(2)如果BC=BD,AE·AF=AD·BF,求证:△ABE∽△ACD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线![]() 经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2, 0),则点C的坐标为( )
经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2, 0),则点C的坐标为( )

A.(﹣1,![]() )B.(﹣2,
)B.(﹣2,![]() )C.(
)C.(![]() ,1)D.(
,1)D.(![]() ,2)
,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
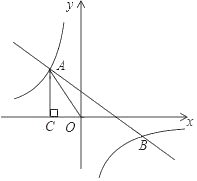
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第二、四象限内的点
的图象交于第二、四象限内的点![]() 和点
和点![]() .过点
.过点![]() 作
作![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,
,![]() 的面积为4.
的面积为4.
(1)分别求出![]() 和
和![]() 的值;
的值;
(2)结合图象直接写出![]() 的解集;
的解集;
(3)在![]() 轴上取点
轴上取点![]() ,使
,使![]() 取得最大值时,求出点
取得最大值时,求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y1=2x2与坐标轴交于A、B两点,与双曲线y2=![]() (x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论错误的是( )
(x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论错误的是( )

A. 当x>0时,y1随x的增大而增大,y2随x的增大而减小;
B. k=4
C. 当0<x<2时,y1<y2
D. 当x=4时,EF=4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x轴下方的部分沿x轴翻折,得到一个新函数的图象(图中的“V形折线”).

(1)类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;
(2)如图2,双曲线y=![]() 与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
①试求△PAD的面积的最大值;
②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点D恰好为BC的中点,过点D作⊙O的切线交AC边于点F.

(1)求证:DF⊥AC;
(2)若∠ABC=30°,求tan∠BCO的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD是AC边上的高,点E在边AB上,联结CE交BD于点O,且![]() ,AF是∠BAC的平分线,交BC于点F,交DE于点G.
,AF是∠BAC的平分线,交BC于点F,交DE于点G.
(1)求证:CE⊥AB.
(2)求证:![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com