
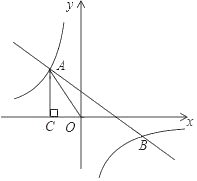
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第二、四象限内的点
的图象交于第二、四象限内的点![]() 和点
和点![]() .过点
.过点![]() 作
作![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,
,![]() 的面积为4.
的面积为4.
(1)分别求出![]() 和
和![]() 的值;
的值;
(2)结合图象直接写出![]() 的解集;
的解集;
(3)在![]() 轴上取点
轴上取点![]() ,使
,使![]() 取得最大值时,求出点
取得最大值时,求出点![]() 的坐标.
的坐标.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
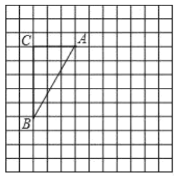
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.![]() 的三个顶点
的三个顶点![]() 、
、![]() 、
、![]() 都在格点上,将
都在格点上,将![]() 绕点
绕点![]() 逆时针方向旋转
逆时针方向旋转![]() 得到
得到![]() ;
;
(1)在正方形网格中,画出![]() ;
;
(2)分别画出旋转过程中,点![]() 和点
和点![]() 经过的路径,并计算点
经过的路径,并计算点![]() 所走过的路径的长度;
所走过的路径的长度;
(3)计算线段![]() 在变换到
在变换到![]() 的过程中扫过区域的面积.
的过程中扫过区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=90°
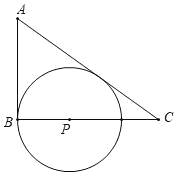
(1)在BC边上找一点P,作⊙P与AC,AB边都相切,与AC的切点为Q;(尺规作图,保留作图痕迹)
(2)若AB=4,AC=6,求第(1)题中所作圆的半径;
(3)连接BQ,第(2)题中的条件不变,求cos∠CBQ的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两转盘分别标有数字。转盘一被三等分,转盘二被分成六份,其中标有数字“8的扇形的圆心角为90°,转动转盘,等旋转停止时,每个转盘上的箭头各指向一个数字(若箭头指向两个扇形的交线,则重新转动转盘,直到指向数字为止).
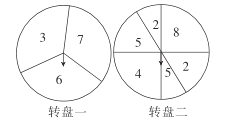
(1)转动转盘一一次,求出指向数字“3”的概率.
(2)同时转动两个转盘,通过画树状图法或列表法求这两个转盘转出的数字之和为偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2﹣5x﹣6在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象,若直线y=2x+b与这个新图象有3个公共点,则b的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
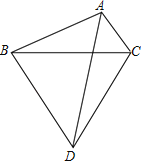
【题目】如图,在△ABC中,∠BAC=120°,以BC为边向外作等边△BCD.
(Ⅰ)∠ABD+∠ACD=_____.
(Ⅱ)∠BAD=_____.
(Ⅲ)若AB=3,AC=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段AB,BC,∠ABC=90°.求作:矩形ABCD.以下是甲、乙两同学的作业:
甲:(1)以点C为圆心,AB长为半径画弧;
(2)以点A为圆心,BC长为半径画弧;
(3)两弧在BC上方交于点D,连接AD,CD,四边形ABCD即为所求(如图1)
乙:(1)连接AC,作线段AC的垂直平分线,交AC于点M;
(2)连接BM并延长,在延长线上取一点D,使MD=MB,连接AD,CD,四边形ABCD即为所求(如图2).
对于两人的作业,下列说法正确的是( )


A. 两人都对 B. 两人都不对 C. 甲对,乙不对 D. 甲不对,乙对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=(m+2)x2-2(m+2)x-m+5,其中m+2>0
(1)求该二次函数的对称轴方程;
(2)过动点C(0,n)作直线1⊥y轴
①当直线1与抛物线只有一个公共点时,求n与m的函数关系;
②若抛物线与x轴有两个交点,将抛物线在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.当n=7时,直线1与新的图象恰好有三个公共点,求此时m的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系内,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴相交于点
轴相交于点![]() 和点
和点![]() ,直线
,直线![]() 为过点
为过点![]() 的旋转直线,交线段
的旋转直线,交线段![]() 于点
于点![]() ,直线
,直线![]() 与
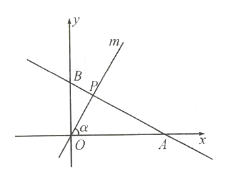
与![]() 轴的正半轴的夹角为
轴的正半轴的夹角为![]() .
.
(1)当直线![]() 旋转到与线段
旋转到与线段![]() 垂直时,求
垂直时,求![]() 的值;
的值;
(2)当直线![]() 旋转到过线段
旋转到过线段![]() 中点时,求
中点时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com