
【题目】为了庆祝“五四”青年节,某校举行了书法比赛,赛后随机抽查部分参赛同学的成绩,并制作成图表如下:
分数段 | 频数 | 频率 |
| 30 | 0.15 |
|
| 0.45 |
| 60 |
|
| 20 | 0.1 |
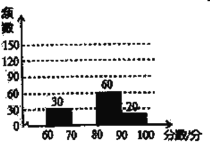
请根据以上图表提供的信息,解答下列问题:
(1)这次随机抽査了_______名学生;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段![]() 所对应扇形的圆心角的度数是________;
所对应扇形的圆心角的度数是________;
(4)全校共有600名学生参加比赛,估计该校成绩![]() 范围内的学生有多少人?
范围内的学生有多少人?
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点B按逆时针方向旋转得到△EBD,点E、点D分别与点A、点C对应,且点D在边AC上,边DE交边AB于点F,△BDC∽△ABC.已知![]() ,AC=5,那么△DBF的面积等于_____.
,AC=5,那么△DBF的面积等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB为直角,AB=10,![]() °,半径为1的动圆Q的圆心从点C出发,沿着CB方向以1个单位长度/秒的速度匀速运动,同时动点P从点B出发,沿着BA方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PB长为半径的⊙P与AB、BC的另一个交点分别为E、D,连结ED、EQ.
°,半径为1的动圆Q的圆心从点C出发,沿着CB方向以1个单位长度/秒的速度匀速运动,同时动点P从点B出发,沿着BA方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PB长为半径的⊙P与AB、BC的另一个交点分别为E、D,连结ED、EQ.
(1)判断并证明ED与BC的位置关系,并求当点Q与点D重合时t的值;
(2)当⊙P和AC相交时,设CQ为![]() ,⊙P被AC 截得的弦长为
,⊙P被AC 截得的弦长为![]() ,求
,求![]() 关于
关于![]() 的函数; 并求当⊙Q过点B时⊙P被AC截得的弦长;
的函数; 并求当⊙Q过点B时⊙P被AC截得的弦长;
(3)若⊙P与⊙Q相交,写出t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在AD边上,点F在AD的延长线上,且BE=CF.
(1)求证:四边形EBCF是平行四边形.
(2)若∠BEC=90°,∠ABE=30°,AB=![]() ,求ED的长.
,求ED的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (点
(点![]() 在点
在点![]() 的左侧),对称轴与
的左侧),对称轴与![]() 轴交于点(3,0),且
轴交于点(3,0),且![]() .
.
(1)求抛物线![]() 的表达式及顶点坐标;
的表达式及顶点坐标;
(2)将抛物线![]() 平移,得到的新抛物线
平移,得到的新抛物线![]() 的顶点为(0,﹣1),抛物线
的顶点为(0,﹣1),抛物线![]() 的对称轴与两条抛物线
的对称轴与两条抛物线![]() ,
,![]() 围成的封闭图形为
围成的封闭图形为![]() .直线
.直线![]() 经过点
经过点![]() .若直线
.若直线![]() 与图形
与图形![]() 有公共点,求
有公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是边AC上一点,联结BD,给出下列条件:∠ABD=∠ACB;②AB2=ADAC;③ADBC=ABBD;④ABBC=ACBD.其中单独能够判定△ABD∽△ACB的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB = 4,BC = 5,点P在边AC上,且![]() ,联结BP,以BP为一边作△BPQ(点B、P、Q按逆时针排列),点G是△BPQ的重心,联结BG,∠PBG =∠BCA,∠QBG =∠BAC,联结CQ并延长,交边AB于点M.设PC = x,
,联结BP,以BP为一边作△BPQ(点B、P、Q按逆时针排列),点G是△BPQ的重心,联结BG,∠PBG =∠BCA,∠QBG =∠BAC,联结CQ并延长,交边AB于点M.设PC = x,![]() .
.
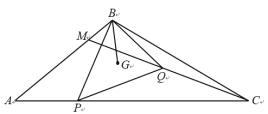
(1)求![]() 的值;
的值;
(2)求y关于x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三张“黑桃”扑克牌,背面完全相同将三张扑克牌背面朝上,洗匀后放在桌面上甲,乙两人进行摸牌游戏,甲先从中随机抽取一张,记下数字再放回洗匀,乙再从中随机抽取一张.

(1)甲抽到“黑桃”,这一事件是 事件(填“不可能“,“随机“,“必然”);
(2)利用树状图或列表的方法,求甲乙两人抽到同一张扑克牌的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH,FG.
(1)求证:△BFH≌△DEG;
(2)连接DF,若BF=DF,则四边形EGFH是什么特殊四边形?证明你的结论.
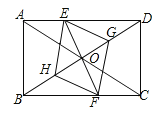
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com