
分析 首先化简(2x+y)2+(x-y)(x+y)-5x(x-y),然后把x=$\sqrt{2}$+1,y=$\sqrt{2}$-1代入化简后的算式,求出算式的值是多少即可.
解答 解:(2x+y)2+(x-y)(x+y)-5x(x-y)
=4x2+4xy+y2+x2-y2-5x2+5xy
=9xy
当x=$\sqrt{2}$+1,y=$\sqrt{2}$-1时,
原式=9($\sqrt{2}$+1)($\sqrt{2}$-1)
=9×(2-1)
=9×1
=9
点评 此题主要考查了整式的混合运算-化简求值问题,要熟练掌握,解答此题的关键是要明确:先按运算顺序把整式化简,再把对应字母的值代入求整式的值.


科目:初中数学 来源: 题型:解答题
| 成绩x 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
| 甲 | 0 | 0 | 1 | 11 | 7 | 1 |
| 乙 | 1 | 0 | 0 | 7 | 10 | 2 |
| 部门 | 平均数 | 中位数 | 众数 |
| 甲 | 78.3 | 77.5 | 75 |
| 乙 | 78 | 80.5 | 81 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
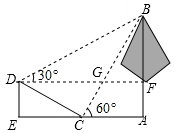 如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10m,则树AB的高度是( )m.
如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10m,则树AB的高度是( )m.| A. | 20$\sqrt{3}$ | B. | 30 | C. | 30$\sqrt{3}$ | D. | 40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com