
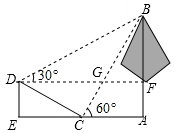
 如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10m,则树AB的高度是( )m.
如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10m,则树AB的高度是( )m.| A. | 20$\sqrt{3}$ | B. | 30 | C. | 30$\sqrt{3}$ | D. | 40 |
分析 先根据CD=20米,DE=10m得出∠DCE=30°,故可得出∠DCB=90°,再由∠BDF=30°可知∠DBE=60°,由DF∥AE可得出∠BGF=∠BCA=60°,故∠GBF=30°,所以∠DBC=30°,再由锐角三角函数的定义即可得出结论.
解答 解:在Rt△CDE中,
∵CD=20m,DE=10m,
∴sin∠DCE=$\frac{10}{20}$=$\frac{1}{2}$,
∴∠DCE=30°.
∵∠ACB=60°,DF∥AE,
∴∠BGF=60°
∴∠ABC=30°,∠DCB=90°.
∵∠BDF=30°,
∴∠DBF=60°,
∴∠DBC=30°,
∴BC=$\frac{CD}{tan30°}$=$\frac{20}{\frac{\sqrt{3}}{3}}$=20$\sqrt{3}$m,
∴AB=BC•sin60°=20$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=30m.
故选B.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,熟记锐角三角函数的定义是解答此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 4 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
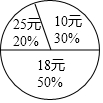 某餐厅供应单价为10元、18元、25元三种价格的抓饭,如图是该餐厅某月销售抓饭情况的扇形统计图,根据该统计图可算得该餐厅销售抓饭的平均单价为17元.
某餐厅供应单价为10元、18元、25元三种价格的抓饭,如图是该餐厅某月销售抓饭情况的扇形统计图,根据该统计图可算得该餐厅销售抓饭的平均单价为17元.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
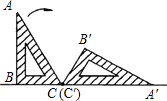 如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C′的位置,若BC=12cm,则顶点A从开始到结束所经过的路径长为16πcm.
如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C′的位置,若BC=12cm,则顶点A从开始到结束所经过的路径长为16πcm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com