
【题目】如图,在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点(点
上的点(点![]() 不与端点
不与端点![]() 重合),且
重合),且![]() ,连接
,连接![]() 并取
并取![]() 的中点
的中点![]() ,连接
,连接![]() 并延长至点
并延长至点![]() ,使
,使![]() ,连接
,连接![]() .
.

(1)求证:四边形![]() 是正方形;
是正方形;
(2)当点![]() 在什么位置是,四边形
在什么位置是,四边形![]() 的面积最小?并求四边形
的面积最小?并求四边形![]() 面积的最小值.
面积的最小值.
【答案】(1)见解析;(2)当点E为线段AC的中点时,四边形EDFG的面积最小,该最小值为4.
【解析】
试题分析:(1)连接CD,根据等腰直角三角形的性质可得出∠A=∠DCF=45°、AD=CD,结合AE=CF可证出△ADE≌△CDF(SAS),根据全等三角形的性质可得出DE=DF、ADE=∠CDF,通过角的计算可得出∠EDF=90°,再根据O为EF的中点、GO=OD,即可得出GD⊥EF,且GD=2OD=EF,由此即可证出四边形EDFG是正方形;
(2)过点D作DE′⊥AC于E′,根据等腰直角三角形的性质可得出DE′的长度,从而得出2≤DE<2![]() ,再根据正方形的面积公式即可得出四边形EDFG的面积的最小值.
,再根据正方形的面积公式即可得出四边形EDFG的面积的最小值.
试题解析:(1)证明:连接CD,如图1所示.
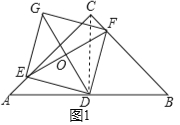
∵△ABC为等腰直角三角形,∠ACB=90°,D是AB的中点,
∴∠A=∠DCF=45°,AD=CD.
在△ADE和△CDF中,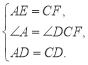 ,
,
∴△ADE≌△CDF(SAS),∴DE=DF,∠ADE=∠CDF.
∵∠ADE+∠EDC=90°,∴∠EDC+∠CDF=∠EDF=90°,
∴△EDF为等腰直角三角形.
∵O为EF的中点,GO=OD,∴GD⊥EF,且GD=2OD=EF,
∴四边形EDFG是正方形;
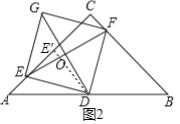
(2)解:过点D作DE′⊥AC于E′,如图2所示.
∵△ABC为等腰直角三角形,∠ACB=90°,AC=BC=4,
∴DE′=![]() BC=2,AB=4
BC=2,AB=4![]() ,点E′为AC的中点,
,点E′为AC的中点,
∴2≤DE<2![]() (点E与点E′重合时取等号).
(点E与点E′重合时取等号).
∴4≤S四边形EDFG=DE2<8.
∴当点E为线段AC的中点时,四边形EDFG的面积最小,该最小值为4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的两条对角线相交于点O,点E是AB边的中点,图中已有三角形与△ADE面积相等的三角形(不包括△ADE)共有( )个. 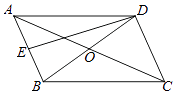
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面调查适合利用选举的形式进行数据收集的是( )
A. 谁在电脑福利彩票中中一等奖
B. 10月1日是什么节日
C. 谁在某地2013年中考中取得第一名
D. 谁最适合当文艺委员
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
(1)求这两个函数的表达式;
(2)根据图象直接写出一次函数的值大于反比例函数的值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学著作中有这样一道题:“远望巍巍塔七层,红光点点倍加增共灯三百八十一,请问尖头几盏灯”.意思是:远远望见一座7层高的雄伟壮丽的佛塔,每层塔点着的红灯数,下层比上层成倍增加,共381盏.则塔尖有______盏灯.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com