
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H.给出下列结论:
①△ABE≌△DCF;②![]() ;③DP2=PHPB;④
;③DP2=PHPB;④![]() .
.
其中正确的是____________.(写出所有正确结论的序号)
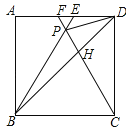
【答案】①③④.
【解析】
试题∵△BPC是等边三角形,∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,在正方形ABCD中,∵AB=BC=CD,∠A=∠ADC=∠BCD=90°,∴∠ABE=∠DCF=30°,在△ABE与△CDF中,∵∠A=∠ADC,∠ABE=∠DCF,AB=CD,∴△ABE≌△DCF,故①正确;
∵PC=CD,∠PCD=30°,∴∠PDC=75°,∴∠FDP=15°,∵∠DBC=45°,∴∠PBD=15°,∴∠FDP=∠PBD,∵∠DFP=∠BPC=60°,∴△DFP∽△BPH,∴![]() ,故②错误;
,故②错误;
∵∠PDH=∠PCD=30°,∵∠DPH=∠DPC,∴△DPH∽△CPD,∴![]() ,∴
,∴![]() ,∵PB=CD,∴
,∵PB=CD,∴![]() ,故③正确;
,故③正确;
如图,过P作PM⊥CD,PN⊥BC,设正方形ABCD的边长是4,△BPC为正三角形,∴∠PBC=∠PCB=60°,PB=PC=BC=CD=4,∴∠PCD=30°∴PN=PBsin60°=4×![]() =
=![]() ,PM=PCsin30°=2,S△BPD=S四边形PBCD﹣S△BCD=S△PBC+S△PDC﹣S△BCD=
,PM=PCsin30°=2,S△BPD=S四边形PBCD﹣S△BCD=S△PBC+S△PDC﹣S△BCD=![]() ,∴
,∴![]() .故答案为:①③④.
.故答案为:①③④.



科目:初中数学 来源: 题型:
【题目】请将下列事件发生的概率标在图中:
(1)从高处抛出的物体必落到地面;
(2)从装有![]() 个红球的袋子中任取一个,取出的球是白球;
个红球的袋子中任取一个,取出的球是白球;
(3)月亮绕着地球转;
(4)从装有![]() 个红球、
个红球、![]() 个白球的口袋中任取一个球,恰好是红球(这些球除颜色外完全相同);
个白球的口袋中任取一个球,恰好是红球(这些球除颜色外完全相同);
(5)三名选手抽签决定比赛顺序(有三个签,分别写有![]() ,
,![]() ,
,![]() ),抽到写有
),抽到写有![]() 的签.
的签.
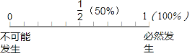
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想![]() 转化,把未知转化为已知.
转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
(1)问题:方程x3+x2-2x=0的解是x1=0,x2= ,x3= ;
(2)拓展:用“转化”思想求方程![]() 的解;
的解;
(3)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
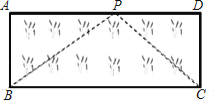
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,在等边△ABC 中,AD是∠BAC的平分线,一个含有120°角的△MPN的顶点P(∠MPN=120°)与点D重合,一边与AB垂直于点E,另一边与AC交于点F.
①请猜想并写出AE+AF与AD之间满足的数量关系,不必证明.
②在图1的基础上,若△MPN绕着它的顶点P旋转,E、F仍然是△MPN的两边与AB、AC的交点,当三角形纸板的边不与AB垂直时,如图2,(1)中猜想是否仍然成立?说明理由.
③如图 3,若△MPN绕着它的顶点P旋转,当△MPN的一边与AB的延长线相交,另一边与AC的反向延长线相交时,AE、AF与AD之间又满足怎样的数量关系?直接写出结论,不必证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】牛奶是最古老的天然饮料之一,被誉为“白色血液”,对人体的重要性可想而知,现已成为国家营养餐计划备选食品之一.为推行国家营养餐计划,某乳品公司向某营养餐中心运输一批牛奶,由铁路运输每千克只需运费0.58 元;由公路运输,每千克需运费0.28元,还需其他费用600元.请探究选用哪种运输方式所需费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边的中点,DE⊥BC交AB于点E,AD=AC,EC交AD于点F.
(1)求证:△ABC∽△FCD;
(2)求证:FC=3EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′OP=r2,则称点P′是点P关于⊙O的“反演点”.
如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为节约水资源,从2018年1月1日起调整居民用水价格,每立方米水费比2017年上涨![]() .小明家2017年8月的水费是18元,而2018年8月的水费是33元.已知小明家2018年8月的用水量比2017年8月的用水量多5 m3.
.小明家2017年8月的水费是18元,而2018年8月的水费是33元.已知小明家2018年8月的用水量比2017年8月的用水量多5 m3.
(1)求该市2017年居民用水的价格;
(2)小明家2019年8月用水量比2018年8月份用水量多了20%,求小明家2019年8月份的水费.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com