Question

【题目】如图所示，正方形ABCD的边长为8，M在DC上，且DM=2，N是AC上的一动点，求DN+MN的最小值．

Answer 1

【答案】解：如图，连接BM，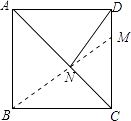
∵点B和点D关于直线AC对称，
∴NB=ND，
则BM就是DN+MN的最小值，
∵正方形ABCD的边长是8，DM=2，
∴CM=6，
∴BM= =10，
∴DN+MN的最小值是10．
【解析】要求DN+MN的最小值，DN，MN不能直接求，可考虑通过作辅助线转化DN，MN的值，从而找出其最小值求解．
【考点精析】解答此题的关键在于理解正方形的性质的相关知识，掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形，以及对轴对称-最短路线问题的理解，了解已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径．