练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    从菱形的钝角顶点向对角的两条边作垂线，垂足恰好是该边的中点，则菱形的内角中钝角的度数是（     ）

    A.150°             B. 135°          C. 120°              D. 100°


    C  解析：如图，连接AC.在菱形ABCD中，AD=DC,AE⊥CD， AF⊥BC，因为，所以AE是CD的中垂线，所以，所以△ADC是等边三角形，所以∠60°，从而∠120°.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，以点O为位似中心，将△ABC放大得到△DEF．若AD=OA，则△ABC与△DEF的面积之比为（　　）

    　

    A．

    1：2

    B．

    1：4

    C．

    1：5

    D．

    1：6

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    阅读资料：

    如图1，在平面之间坐标系xOy中，A，B两点的坐标分别为A（x1，y1），B（x2，y2），由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2，所以A，B两点间的距离为AB= ．

    我们知道，圆可以看成到圆心距离等于半径的点的集合，如图2，在平面直角坐标系xoy中，A（x，y）为圆上任意一点，则A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2，当⊙O的半径为r时，⊙O的方程可写为：x2+y2=r2．

    问题拓展：如果圆心坐标为P（a，b），半径为r，那么⊙P的方程可以写为　（ 综合应用：

    如图3，⊙P与x轴相切于原点O，P点坐标为（0，6），A是⊙P上一点，连接OA，使tan∠POA=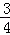，作PD⊥OA，垂足为D，延长PD交x轴于点B，连接AB．

    ①证明AB是⊙P的切点；

    ②是否存在到四点O，P，A，B距离都相等的点Q？若存在，求Q点坐标，并写出以Q为圆心，以OQ为半径的⊙O的方程；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若矩形的长是，宽是，一个正方形的面积等于该矩形的面积，则正方形的边长是_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在长为，宽为的矩形的四个角上截去四个全等的小正方形，使得留下的图形（图中阴影部分）的面积是原矩形面积的80％，求所截去的小正方形的边长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    矩形、菱形、正方形都具有的性质是（　　）

    A.每一条对角线平分一组对角       B.对角线相等

    C.对角线互相平分                  D.对角线互相垂直

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，正方形ABCD的边长为4，E为BC上的一点，BE=1，F为AB上的一点，AF=2，P为AC上一个动点，则PF+PE的最小值为        .

    第15题图

    查看答案和解析>>

    科目：初中数学 来源： 题型：


      “抛一枚均匀硬币，落地后正面朝上”.这一事件是……………………………（   ）

    A.  随机事件       B. 确定事件        C. 必然事件        D.  不可能事件

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知：如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于点D.

    求证：BE=CD．



    查看答案和解析>>

    同步练习册答案