练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知：如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于点D.

    求证：BE=CD．




     证明：∵BE⊥CE，AD⊥CE，

    ∴∠BEC=∠CDA＝90°. ………………………1分

    ∴∠EBC＋∠ECB＝90°.

    又∵∠DCA＋∠ECB＝90°，

    ∴∠EBC=∠DCA. ………………………………2分

    又∵BC=AC，……………………………………3分

    ∴△BEC≌△CDA. ………………………………………………………………4分

    ∴BE＝CD.  ………………………………………………………………………5分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    从菱形的钝角顶点向对角的两条边作垂线，垂足恰好是该边的中点，则菱形的内角中钝角的度数是（     ）

    A.150°             B. 135°          C. 120°              D. 100°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若直线y＝m（m为常数）与函数y＝的图象恒有三个不同的交点，则常数m的取值范围是       ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在一个不透明的盒子中装有n个小球，它们除了颜色不同外，其余都相同，其中有4个

    白球，每次试验前，将盒子中的小球摇匀，随机摸出一个球记下颜色后再放回盒中.

    大量重复上述试验后发现，摸到白球的频率稳定在0.4，那么可以推算出n大约是

    A . 10                  B. 14                C. 16                D. 40

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    分解因式：                  ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    查看答案和解析>>

    科目：初中数学 来源： 题型：


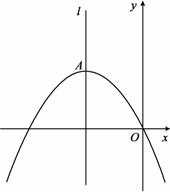    如图，顶点为A（－4,4）的二次函数图象经过原点（0,0），点P在该图象上，OP交其对称轴l于点M，点M、N关于点A对称，连接PN，ON.

    （1）求该二次函数的表达式；

    （2）若点P的坐标是（－6,3），求△OPN的面积；

    （3）当点P在对称轴l左侧的二次函数图象上运动时，

    请解答下面问题：

           ① 求证：∠PNM＝∠ONM；

    ② 若△OPN为直角三角形，请直接写出所有符合

    条件的点P的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年福建省七年级上学期期末考试数学试卷（解析版） 题型：解答题

    （本小题8分）如图，∠AOB=∠COD=90°，OC平分∠AOB，OE是∠BOD的三等分线．

    （1）求∠BOD的度数；

    （2）求∠COE的度数．

    查看答案和解析>>

    同步练习册答案