
【题目】在矩形ABCD中,AB=1,BC=2,点P是边BC上一点(点P不与点B,点C重合),点C关于直线AP的对称点为C'.
(1)如果C'落在线段AB的延长线上.
①在图①中补全图形;
②求线段BP的长度;
(2)如图②,设直线AP与CC'的交点为M,求证:BM⊥DM.

【答案】(1)①见解析;②PB=![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)①根据要求画出图形即可;
②连接AC,作PH⊥AC于H.则△APB≌△APH,同侧AB=AH=1,PB=PH,设PB=PH=x,利用勾股定理构建方程即可;
(2)如图②中,连接AC、BD交于点O.连接OM.只要证明A、B、M、C、D五点共圆,即可解决问题;
解:(1)①如图①所示:
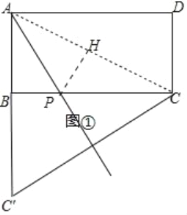
②连接AC,作PH⊥AC于H.则△APB≌△APH,
∴AB=AH=1,PB=PH,设PB=PH=x,
∵AC=![]() =
=![]() ,
,
∴CH=![]() ﹣1,
﹣1,
在Rt△PCH中,x2+(![]() ﹣1)2=(2﹣x)2,
﹣1)2=(2﹣x)2,
解得x=![]() ,
,
∴PB=![]() .
.
(2)如图②中,连接AC、BD交于点O.连接OM.
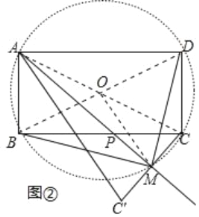
∵四边形ABCD是矩形,
∴OA=OB=OC=OD,
∵∠AMC=90°,
∴OM=OA=OB=OC=OD,
∴A、B、M、C、D五点共圆,
∵BD是直径,
∴∠BMD=90°,
∴BM⊥DM.


科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有红、黄、白三种颜色的球共10个,它们除了颜色外完全相同,其中黄球个数比白球个数的3倍少2个,从袋中摸出一个球是黄球的概率为0.4.
(1)求袋中红、黄、白三种颜色的球的个数;
(2)向袋中放入若干个红球,使摸出一个球是红球的概率为0.7,求放入红球的个数;
(3)在(2)的条件下,求摸出一个球是白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)3![]() +(
+(![]() )+(
)+(![]() )+(
)+(![]() );
);
(2)25.7+(-7.3)+(-13.7)+7.3;
(3)(-2.125)+(![]() )+(
)+(![]() )+(-3.2);
)+(-3.2);
(4)(-0.8)+6.4+(-9.2)+3.6+(-1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,BE=1,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则EC的长为( )
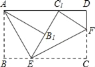
A. ![]() B. 2 C. 3 D. 2
B. 2 C. 3 D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划组织师生共435人参加一次大型公益活动,如果租用5辆小客车和6辆大客车恰好全部坐满,已知每辆大客车的乘客座位数比小客车多12个.
(1) 求每辆小客车和每辆大客车的乘客座位数;
(2) 由于最后参加活动的人数增加了20人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完成,求租用小客车数量的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校奖励学生,初一获奖学生中,有一人获奖品3件,其余每人获奖品7件;初二获奖学生中,有一人获奖品4件,其余每人获奖品9件.如果两个年级获奖人数不等,但奖品数目相等,且每个年级奖品数大于50而不超过100,那么两个年级获奖学生共有_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形;(直接写出答案,不需要说明理由)
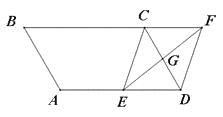
查看答案和解析>>
科目:初中数学 来源: 题型:
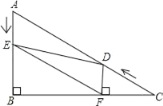
【题目】如图,在Rt△ABC中,∠B=90°,BC=![]() ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)AC的长是 ,AB的长是 .
(2)在D、E的运动过程中,线段EF与AD的关系是否发生变化?若不变化,那么线段EF与AD是何关系,并给予证明;若变化,请说明理由.
(3)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了调查同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取部分同学进行问卷测试,把测试成绩分成“优、良、中、差”四个等级,绘制了如下不完整的统计图:

根据以上统计信息,解答下列问题:
(1)求成绩是“优”的人数占抽取人数的百分比;
(2)求本次随机抽取问卷测试的人数;
(3)请把条形统计图补充完整;
(4)若该校学生人数为3000人,请估计成绩是“优”和“良”的学生共有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com