
【题目】我市某镇组织20辆汽车装运完![]() 三种品牌脐橙共100吨参加上海世博会,按计划,20辆汽车都要装运,每辆汽车只能装运用一种脐橙,且必须装满。根据下表提供的信息,解答以下问题:
三种品牌脐橙共100吨参加上海世博会,按计划,20辆汽车都要装运,每辆汽车只能装运用一种脐橙,且必须装满。根据下表提供的信息,解答以下问题:
从A,B两地运往甲,乙两地的费用如下表:
脐橙品种 | A | B | C |
每辆汽车运载量(吨) | 6 | 5 | 4 |
每吨脐橙获利(百元) | 12 | 16 | 10 |
(1)设装运![]() 种脐橙的车辆数为
种脐橙的车辆数为![]() ,装运
,装运![]() 种脐橙的车辆数为
种脐橙的车辆数为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果装运每种脐橙的车辆数都不少于4辆,那么车辆的安排方案有几种?并写出每种安排方案?
(3)若要使此次销售获利最大,应采用哪种安排方案?请求出最大利润的值
【答案】(1)y=20-2x;(2)详见解析;(3)当装运A种脐橙4车、B种脐橙12车、C种脐橙4车时,获利最大,最大利润为14.08万元。
【解析】
(1)等量关系为:车辆数之和=20;
(2)关系式为:装运每种脐橙的车辆数≥4;
(3)总利润为:装运A种脐橙的车辆数×6×12+装运B种脐橙的车辆数×5×16+装运C种脐橙的车辆数×4×10,然后按x的取值来判定.
解:(1)根据题意,装运A种脐橙的车辆数为x,装运B种脐橙的车辆数为y,
那么装运C种脐橙的车辆数为(20-x-y),
则有:6x+5y+4(20-x-y)=100
整理得:y=-2x+20(1≤x≤9且为整数);
(2)由(1)知,装运A、B、C三种脐橙的车辆数分别为x,-2x+20,x.
由题意得![]()
解得:4≤x≤8
因为x为整数,
所以x的值为4,5,6,7,8,所以安排方案共有5种.
方案一:装运A种脐橙4车,B种脐橙12车,C种脐橙4车;
方案二:装运A种脐橙5车,B种脐橙10车,C种脐橙5车,
方案三:装运A种脐橙6车,B种脐橙8车,C种脐橙6车,
方案四:装运A种脐橙7车,B种脐橙6车,C种脐橙7车,
方案五:装运A种脐橙8车,B种脐橙4车,C种脐橙8车;
(3)设利润为W(百元)则:W=6x×12+5(-2x+20)×16+4x×10=-48x+1600
∵k=-48<0
∴W的值随x的增大而减小.
要使利润W最大,则x=4,
故选方案一W最大=-48×4+1600=1408(百元)=14.08(万元)
答:当装运A种脐橙4车,B种脐橙12车,C种脐橙4车时,获利最大,最大利润为14.08万元.


科目:初中数学 来源: 题型:
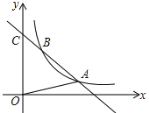
【题目】如图,一次函数的图象与y轴交于C(0,8),且与反比例函数y=![]() (x>0)的图象在第一象限内交于A(3,a),B(1,b)两点.
(x>0)的图象在第一象限内交于A(3,a),B(1,b)两点.
⑴求△AOC的面积;
⑵若![]() =4,求反比例函数和一次函数的解析式.
=4,求反比例函数和一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,对角线AC,BD交于点O,E是边AD上的一个动点(与点A,D不重合),连接EO并延长,交BC于点F,连接BE,DF.下列说法:
① 对于任意的点E,四边形BEDF都是平行四边形;
② 当∠ABC>90°时,至少存在一个点E,使得四边形BEDF是矩形;
③ 当AB<AD时,至少存在一个点E,使得是四边形BEDF是菱形;
④ 当∠ADB=45°时,至少存在一个点E,使得是四边形BEDF是正方形.
所有正确说法的序号是:_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠BAD=100°,∠B=∠D=90°,在BC、CD上分别找一个点M、N,使△AMN的周长最小,则∠AMN+∠ANM的度数为( )

A.130°B.120°C.160°D.100°
查看答案和解析>>
科目:初中数学 来源: 题型:
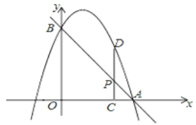
【题目】如图,已知抛物线![]() 分别交x轴、y轴于点A(2,0)、B(0,4),点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
分别交x轴、y轴于点A(2,0)、B(0,4),点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
(1)若![]() .
.
①求抛物线的解析式;
②当线段PD的长度最大时,求点P的坐标;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形边长为![]() 的网格中,
的网格中,![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 均在格点上,
均在格点上,![]() 为
为![]() 边上的一点.
边上的一点.
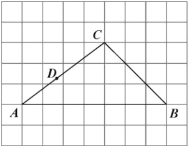
(Ⅰ)线段![]() 的值为______________;
的值为______________;
(Ⅱ)在如图所示的网格中,![]() 是
是![]() 的角平分线,在
的角平分线,在![]() 上求一点
上求一点![]() ,使
,使![]() 的值最小,请用无刻度的直尺,画出
的值最小,请用无刻度的直尺,画出![]() 和点
和点![]() ,并简要说明
,并简要说明![]() 和点
和点![]() 的位置是如何找到的(不要求证明)___________.
的位置是如何找到的(不要求证明)___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
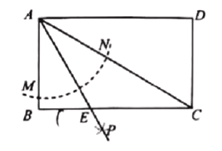
【题目】如图,矩形![]() 以点
以点![]() 为圆心,以任意长为半径作弧分别交
为圆心,以任意长为半径作弧分别交![]() 、
、![]() 于
于![]() 两点,再分别以点
两点,再分别以点![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径作弧交于点
的长为半径作弧交于点![]() ,作射线
,作射线![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则矩形
,则矩形![]() 的面积等于__________.
的面积等于__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上一点.F是线段BC延长线上一点,且CF=AE连接BE

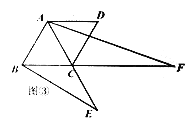
(1)发现问题:如图①,若E是线段AC的中点,连接EF,其他条件不变,猜想线段BE与EF的数量关系
(2)探究问题:如图②,若E是线段AC上任意一点,连接EF,其他条件不变,猜想线段BE与EF的数量关系是什么?请证明你的猜想
(3)解决问题:如图③,若E是线段AC延长线上任意一点,其他条件不变,且∠EBC=30°,AB=3请直接写出AF的长度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com