
分析 54张牌按照下面的分成四个部分:大王和小王、1-6、7和8、9-13,考虑最差情况:怎么取得最多的牌而没有任何两张牌之和等于15呢?在这四个部分里,当取到1-6区间的时候,就不能取8-13区间的牌,反之一样;而且7只能取一个,大小王必取.这样我们就可以这样取牌:大小王、1-6全取、1个7(或 大小王、1个7、8-13全取)总共27张牌,依此即可求解.
解答 解:即使数出20张,也不确保能有数出的牌中有两张同花色的牌的点数之和为15.
9,10,11,12,13点的牌一共是20张,A,2,3,4,5点一共也是4花色20张,
抽出的牌正好是这2个组合是怎么也没有两张同花色的牌的点数之和为15.
最多的是7+8=15,
即最少要有一张7和8以上的牌全没被抽走,那么最多只能抽 6×4+3=27张牌(加上大小王也还是27张),
如果剩下的全是 1,3,5,7,9,11,13,大小王,那么也不存在和为15,
所以7×4+2=30,54-30=24,
所以最少只能抽走23张.
故答案为:27,23.
点评 此题考查推理与论证,抽屉原理解决实际问题的灵活应用,要注意考虑最差情况.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
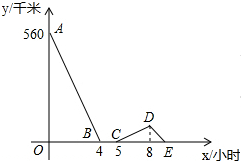 一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象.当快车到达甲地时,慢车离甲地的距离为60千米.
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象.当快车到达甲地时,慢车离甲地的距离为60千米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
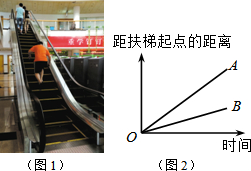 大明因急事在运行中的自动扶梯上行走去二楼(如图1),图2中线段OA、OB分别表示大明在运行中的自动扶梯上行走去二楼和静止站在运行中的自动扶梯上去二楼时,距自动扶梯起点的距离与时间之间的关系.下面四个图中,虚线OC能大致表示大明在停止运行(即静止)的自动扶梯上行走去二楼时,距自动扶梯起点的距离与时间关系的是( )
大明因急事在运行中的自动扶梯上行走去二楼(如图1),图2中线段OA、OB分别表示大明在运行中的自动扶梯上行走去二楼和静止站在运行中的自动扶梯上去二楼时,距自动扶梯起点的距离与时间之间的关系.下面四个图中,虚线OC能大致表示大明在停止运行(即静止)的自动扶梯上行走去二楼时,距自动扶梯起点的距离与时间关系的是( )| A. | 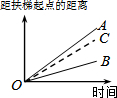 | B. | 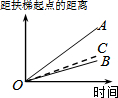 | C. | 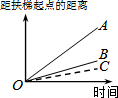 | D. | 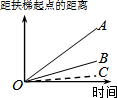 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com