
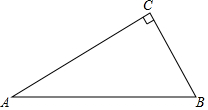
 如图,△ABC是直角三角形,∠ACB=90°,∠A=30°
如图,△ABC是直角三角形,∠ACB=90°,∠A=30°分析 (1)①作线段AB的垂直平分线EF交AB于O,以O为圆心OA为半径作⊙O,⊙O即为所求.②过点C作OC的垂线,交AB的延长线于D,直线CD即为所求;
(2)根据线段CD,BD及$\widehat{BC}$所围成图形的面积=S△DOC-S扇形O-BC计算即可;
解答 解:(1)①作线段AB的垂直平分线EF交AB于O,以O为圆心OA为半径作⊙O,
⊙O即为所求.
②过点C作OC的垂线,交AB的延长线于D,
直线CD即为所求.
(2)线段CD,BD及$\widehat{BC}$所围成图形的面积=S△DOC-S扇形O-BC=$\frac{1}{2}$$•2\sqrt{3}$•6-$\frac{60•π•(2\sqrt{3})^{2}}{360}$=6$\sqrt{3}$-2π.
点评 本题考查作图-复杂作图、三角形的外接圆与外心、切线的判定和性质等知识,解题的关键是熟练掌握基本作图,学会用分割法求面积,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
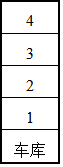 小明、小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至4层的任意一层出电梯.
小明、小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至4层的任意一层出电梯.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象与一次函数y=k2x+b的图象交于A(1,6),B(m,2)两点.
如图,反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象与一次函数y=k2x+b的图象交于A(1,6),B(m,2)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
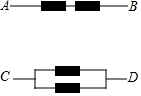 已知电流在一定时间段内正常通过电子元件的概率是0.5,用列表或画树状图的方法分别求在一定时间段内,A、B之间和C、D之间电流能够正常通过的概率.(提示:可用1、0分别表示电子元件的通与不通两种状态)
已知电流在一定时间段内正常通过电子元件的概率是0.5,用列表或画树状图的方法分别求在一定时间段内,A、B之间和C、D之间电流能够正常通过的概率.(提示:可用1、0分别表示电子元件的通与不通两种状态)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com