

���� ��1����������AH=BH=x������BC=4��tanC=3���ɵ�$\frac{4-x}{x}$=3���ⷽ�̼��ɣ�
��2������ͼ����HP��AE��P��HJ��AC��J�����ݡ�EHA�ס�FHC���õ���HP=3AP��AE=2AP���ֱ���Rt��APH��Rt��CHJ�н�ֱ�������μ��ɣ�
�����жϳ���AGQ�ס�CHQ���õ� $\frac{AQ}{GQ}$=$\frac{CQ}{HQ}$��Ȼ���жϳ���AQC�ס�GQH�������Ʊȼ��ɣ�
��� �⣺��1���ߡ�BDH���ɡ�AHC��ת���ã�
��BH=AH����BH=AH=x��
��Rt��ACH��tan��CAH=$\frac{CH}{AH}$=3��
��$\frac{4-x}{x}$=3��
���x=3��
��CH=1��
��2������ͼ����HP��AE��P��HJ��AC��J��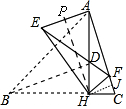
����ת֪����EHF=��BHD=��AHC=90�㣬EH=AH=3��CH=DH=FH��
���EHA=��FHC��$\frac{EH}{AH}$=$\frac{FH}{HC}$=1��
���EHA�ס�FHC��
���EAH=��C��
��tan��EAH=tanC=3��
��HP=3AP��AE=2AP��
��Rt��AHP��AP2+HP2=AH2��
��AP2+��3AP��2=9��
��AP=$\frac{3\sqrt{10}}{10}$��
��AE=$\frac{3\sqrt{10}}{5}$��
��֪�ı���APHJ�Ǿ��Σ�
��HJ=AP=$\frac{3\sqrt{10}}{10}$��
��HF=HC=1��HJ��CF��
��CJ=FJ=$\sqrt{1-��\frac{3\sqrt{10}}{10}��^{2}}$=$\frac{\sqrt{10}}{10}$��
��CF=$\frac{2\sqrt{10}}{10}$��
����ͼ1��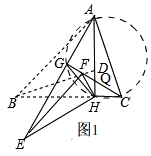
�ߡ�EHF���ɡ�BHD�Ƶ�H��ʱ����ת30��õ���
��HD=HF����AHF=30��
���CHF=90��+30��=120�㣬
�ɢ��У���AEH�͡�FHC��Ϊ���������Σ�
���GAH=��HCG=30�㣬
��CG��AE��
���C��H��G��A�ĵ㹲Բ��
���CGH=��CAH��
��CG��AH���ڵ�Q��
�ߡ�AQC=��GQH��
���AQC�ס�GQH��
��$\frac{AC}{HG}$=$\frac{AQ}{GQ}$=$\frac{1}{sin30��}$=2��
�ߡ�EHF���ɡ�BHD�Ƶ�H��ʱ����ת30��õ���
��EF=BD��
�ɣ�1��֪��BD=AC��
��EF=AC
��$\frac{EF}{HG}$=$\frac{AC}{GH}$=$\frac{AQ}{GQ}$=$\frac{1}{sin30��}$=2��
���� �����Ǽ��α任�ۺ��⣬��Ҫ��������ת�����ʣ�ȫ�������ε����ʺ��ж������������ε����ʺ��ж������ɶ�����������Ǻ��������壬���������ε��ж������ʣ��Ȿ��Ĺؼ����������������ʺ��ж������ã�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 60�� | B�� | 80�� | C�� | 90�� | D�� | 100�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
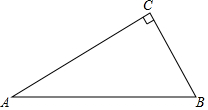 ��ͼ����ABC��ֱ�������Σ���ACB=90�㣬��A=30��
��ͼ����ABC��ֱ�������Σ���ACB=90�㣬��A=30���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{5}{18}$ | D�� | $\frac{11}{36}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com