
【题目】已知二次函数y=﹣x2+bx+c的图象过点A(3,0),C(﹣1,0).
(1)求二次函数的解析式;
(2)如图,点P是二次函数图象的对称轴上的一个动点,二次函数的图象与y轴交于点B,当PB+PC最小时,求点P的坐标;
(3)在第一象限内的抛物线上有一点Q,当△QAB的面积最大时,求点Q的坐标.

【答案】(1)y=﹣x2+2x+3;(2)P(1,2);(3)当m=![]() 时,S最大,此时Q(
时,S最大,此时Q(![]() ,
,![]() ).
).
【解析】
(1)把点A(3,0)、C(-1,0)代入y=-x2+bx+c中,解方程即可得到结论;
(2)连结AB,与对称轴交于点P,此时PB+PC最小.根据抛物线解析式求出B(0,3),利用待定系数法求出直线AB的解析式,于是得到结论;
(3)设Q(m,-m2+2m+3),△QAB的面积为S,连接QA,QB,OQ,根据S=S△OBQ+S△AOQ-S△AOB求出S与m的关系式,利用函数的性质求出m的值,进而得到结论.
(1)把点A(3,0)、C(-1,0)代入y=-x2+bx+c中,
得![]() ,解得
,解得![]() ,
,
则抛物线的解析式为y=-x2+2x+3;
(2)连结AB,与对称轴交于点P,此时PB+PC最小.
在y=-x2+2x+3中,当x=0时,y=3,则B(0,3).
设直线AB的解析式为y=mx+n,
∵A(3,0),B(0,3),
∴![]() ,
,
∴![]() ,
,
∴直线AB的解析式为y=-x+3,
∵y=-x2+2x+3=-(x-1)2+4,
∴对称轴是直线x=1.
当x=1时,y=-1+3=2,
∴P(1,2);
(3)设Q(m,-m2+2m+3),△QAB的面积为S,如图,连接QA,QB,OQ.

则S=S△OBQ+S△AOQ-S△AOB
=![]() ×3m+
×3m+![]() ×3(-m2+2m+3)-
×3(-m2+2m+3)-![]() ×3×3
×3×3
=-![]() m2+
m2+![]() m
m
=-![]() (m-
(m-![]() )2+
)2+![]() ,
,
∴当m═![]() 时,S最大,此时Q(
时,S最大,此时Q(![]() ,
,![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某农场学校积极开展阳光体育活动,组织了九年级学生定点投篮,规定每人投篮3次.现对九年级(1)班每名学生投中的次数进行统计,绘制成如下的两幅统计图,根据图中提供的信息,回答下列问题.
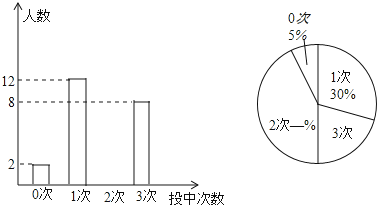
(1)求出九年级(1)班学生人数;
(2)补全两个统计图;
(3)求出扇形统计图中3次的圆心角的度数;
(4)若九年级有学生200人,估计投中次数在2次以上(包括2次)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
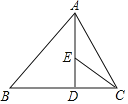
【题目】如图,在△ABC中,∠B=45°,∠ACB=60°,AB=16,AD⊥BC,垂足为D,∠ACB的平分线交AD于点E,则AE的长为( )
A.![]() B.4
B.4![]() C.
C.![]()
![]() D.6
D.6![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
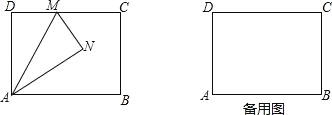
【题目】如图,在矩形 ABCD 中,AB=4,AD=3,M 是边 CD 上一点,将△
ADM 沿直线 AM 对折,得到△AMM.
(1)当 AN 平分∠MAB 时,求 DM 的长;
(2)连接 BN,当 DM=1 时,求 BN 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(2,0)的两条直线![]() ,
,![]() 分别交
分别交![]() 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=![]() .
.

(1)求点B的坐标;
(2)若△ABC的面积为4,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线y=x2﹣3x+c与y轴的交点为(0,2),则下列说法正确的是( )
A. 抛物线开口向下
B. 抛物线与x轴的交点为(﹣1,0),(3,0)
C. 当x=1时,y有最大值为0
D. 抛物线的对称轴是直线x=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程
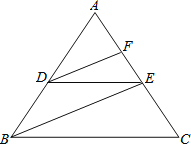
如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:
∵DE∥BC(已知)
∴∠ADE= .( )
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF=![]() ,
,
∠ABE=![]() .( )
.( )
∴∠ADF=∠ABE
∴DF∥ .( )
∴∠FDE=∠DEB. ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确说法的个数有( )
①角是轴对称图形,对称轴是角的平分线;②等腰三角形至少有![]() 条对称轴,至多有
条对称轴,至多有![]() 条对称轴;③关于某直线对称的两个三角形一定是全等三角形;④两图形关于某直线对称,对称点一定在直线的两旁.
条对称轴;③关于某直线对称的两个三角形一定是全等三角形;④两图形关于某直线对称,对称点一定在直线的两旁.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
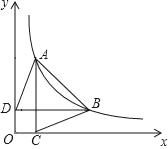
【题目】如图,已知双曲线y=![]() (x>0)图象上两点,过A、B两点分别作x轴、y轴的垂线,垂足分别为C、D,连接AD、BC,则:
(x>0)图象上两点,过A、B两点分别作x轴、y轴的垂线,垂足分别为C、D,连接AD、BC,则:
(1)若A、B两点的坐标分别是(1,4)、(4,1),求S△OAB;
(2)证明:S△ABD=S△ABC.
(3)连接CD,判断CD与AB的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com