
【题目】如图,矩形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 上一点,将
上一点,将![]() 沿
沿![]() 折叠得到
折叠得到![]() ,点
,点![]() 为
为![]() 上一点,将
上一点,将![]() 沿
沿![]() 折叠得到
折叠得到![]() ,且
,且![]() 落在线段
落在线段![]() 上,当
上,当![]() 时,则
时,则![]() 的长为___.
的长为___.
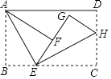
【答案】2
【解析】
由折叠可得∠AEH=![]() ∠BEC=90°,进而得出Rt△AEH中,AE2+EH2=AH2,设BE=x,则EF=x,CE=6-x=EG,再根据勾股定理,即可得到方程x2+42+(6-x)2+(6-2x)2=(2x-2)2+62,解该一元二次方程,即可得到BE的长.
∠BEC=90°,进而得出Rt△AEH中,AE2+EH2=AH2,设BE=x,则EF=x,CE=6-x=EG,再根据勾股定理,即可得到方程x2+42+(6-x)2+(6-2x)2=(2x-2)2+62,解该一元二次方程,即可得到BE的长.
如图,连接AH,
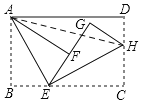
由折叠可得,BE=FE,EC=EG,GH=CH,∠AEB=∠AEF,∠CEH=∠GEH,
∴∠AEH=![]() ∠BEC=90°,
∠BEC=90°,
∴Rt△AEH中,AE2+EH2=AH2,①
设BE=x,则EF=x,CE=6-x=EG,
∴GF=6-2x=GH=CH,DH=4-(6-2x)=2x-2,
∵∠B=∠C=∠D=90°,
∴Rt△ABE中,AE2=EB2+AB2=x2+42,
Rt△CEH中,HE2=EC2+CH2=(6-x)2+(6-2x)2,
Rt△ADH中,AH2=DH2+AD2=(2x-2)2+62,
代入①式,可得
x2+42+(6-x)2+(6-2x)2=(2x-2)2+62,
解得x1=2,x2=12(舍去),
∴BE的长为2,
故答案为:2.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠ADB=90°,AB=2AD,BD的垂直平分线分别交AB,CD于点E,F,垂足为O.
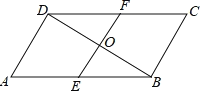
(1)求tan ∠ABD的值;
(2)求证:OE=OF;
(3)连接DE,BF,若AD=6,求DEBF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生的体能情况,体育老师从中随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成尚不完整的扇形图和条形图,根据图形信息回答下列问题:
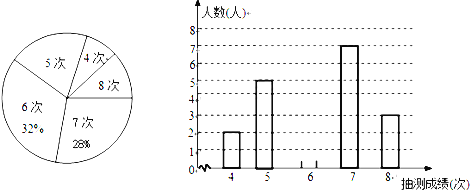
(1)本次抽测的男生有________人,抽测成绩的众数是_________;
(2)请将条形图补充完整;
(3)若规定引体向上6次以上(含6次)为体能达标,则该校125名九年级男生中估计有多少人体能达标?
查看答案和解析>>
科目:初中数学 来源: 题型:
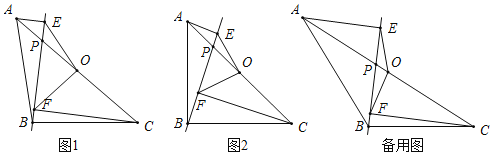
【题目】在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.
(1)如图1,请直接写出线段OE与OF的数量关系;
(2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由
(3)若|CF﹣AE|=2,EF=2![]() ,当△POF为等腰三角形时,请直接写出线段OP的长.
,当△POF为等腰三角形时,请直接写出线段OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
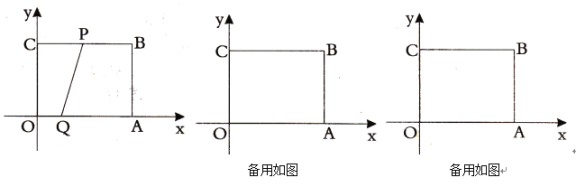
【题目】如图,已知在平面直角坐标系![]() 中,四边形
中,四边形![]() 是矩形,
是矩形,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向以每秒
方向以每秒![]() 个单位长度的速度运动;同时动点
个单位长度的速度运动;同时动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴正半轴方向以每秒
轴正半轴方向以每秒![]() 个单位长度的速度运动.设点
个单位长度的速度运动.设点![]() ,点
,点![]() 的运动时间为
的运动时间为![]() .
.
(1)当![]() 时,按要求回答下列问题
时,按要求回答下列问题
①![]() ______________;
______________;
②求经过![]() ,
,![]() ,
,![]() 三点的抛物线
三点的抛物线![]() 的解析式,若将抛物线
的解析式,若将抛物线![]() 在
在![]() 轴上方的部分图象记为
轴上方的部分图象记为![]() ,已知直线
,已知直线![]() 与
与![]() 有两个不同的交点,求
有两个不同的交点,求![]() 的取值范围;
的取值范围;
(2)连接![]() ,点
,点![]() ,
,![]() 在运动过程中,记
在运动过程中,记![]() 与矩形
与矩形![]() 重叠部分的面积为
重叠部分的面积为![]() ,求
,求![]() 与
与![]() 的函数解析式.
的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
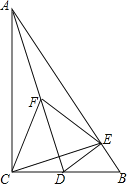
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,D为BC上一点,过点D作DE⊥AB于E.
(1)连接AD,取AD中点F,连接CF,CE,FE,判断△CEF的形状并说明理由
(2)若BD=![]() CD,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,求出n的值.
CD,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,求出n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
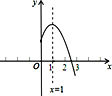
【题目】如图是二次函数![]() (a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2 ,0)和(3 ,0)之间,对称轴是x=1.对于下列结论:① ab<0;② 2a+b=0;③ 3a+c>0;④a+b≥m(am+b)(m为实数);⑤ 当-1<x<3时,y>0. 其中正确结论的个数为( )
(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2 ,0)和(3 ,0)之间,对称轴是x=1.对于下列结论:① ab<0;② 2a+b=0;③ 3a+c>0;④a+b≥m(am+b)(m为实数);⑤ 当-1<x<3时,y>0. 其中正确结论的个数为( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两张长为5,宽为1的矩形纸条交叉,让两个矩形对角线交点重合,且使重叠部分成为一个菱形.当两张纸条垂直时,菱形周长的最小值是4,把一个矩形绕两个矩形重合的对角线交点旋转一定角度,在旋转过程中,得出所有重叠部分为菱形的四边形中,周长的最大值是( )
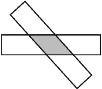
A. 8B. 10C. 10.4D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
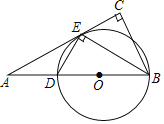
【题目】如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com