
����Ŀ����֪��������A��B��C���㣬�ֱ��ʾ����24����10��10����ֻ�������ϼס��ҷֱ��A��C����ͬʱ������У����ٶ�Ϊ4����λ/�룬�ҵ��ٶ�Ϊ6����λ/�룮
��1���ʼס����������ϵ��ĸ���������
��2���ʶ�������A��B��C����ľ���֮��Ϊ40����λ����
��3�����ס�����ֻ�������ϣ���P��ʾ�����ϡ�Q��ʾ�����ϣ��ֱ��A��C����ͬʱ������У����ٶȱ�Ϊԭ����3�����ҵ��ٶȲ��䣬ֱ��д������ʱ���ԭ��O��������P��������Q�����У���һ��ǡ���������������߶ε��е㣮
![]()
���𰸡��⣺��1����x����������������4x+6x=34��
��� x=3.4��
4��3.4=13.6��-24+13.6=-10.4��
�ʼס����������ϵ�-10.4�������ʴ�Ϊ��-10.4��
��2����y����A��B��C����ľ���֮��Ϊ40����λ��
B���A��C����ľ���Ϊ14+20=34��40��A���B��C����ľ���Ϊ14+34=48��40��C���A��B�ľ���Ϊ34+20=54��40���ʼ�Ӧλ��AB��BC֮�䣮
AB֮��ʱ��4y+��14-4y��+��14-4y+20��=40
���y=2��
BC֮��ʱ��4y+��4y-14��+��34-4y��=40��
���y=5��
�״�A�����˶�2��ʱ���أ���y���������������ʱ�ס��ұ�ʾ��������Ϊͬһ�㣬����ʾ������ͬ��
�ױ�ʾ����Ϊ��-24+4��2-4y���ұ�ʾ����Ϊ��10-6��2-6y��
��������ã�-24+4��2-4y=10-6��2-6y��
��ã�y=7��
�������ʾ����Ϊ��-24+4��2-4y=-44����10-6��2-6y=-44����
���״�A�����˶�5��ʱ���أ���y�������������
�ױ�ʾ����Ϊ��-24+4��5-4y���ұ�ʾ����Ϊ��10-6��5-6y��
��������ã�-24+4��5-4y=10-6��5-6y��
��ã�y=-8������������ȥ����
���״�A�����˶�2��ʱ���أ����������������������������ʾ����Ϊ-44��
��3������x���ԭ��O�Ǽ�����P��������Q������е㣬��
24-12x=10-6x�����x=![]() ��
��
��x���������Q�Ǽ�����P��ԭ��O������е㣬��
24-12x=2��6x-10�������x=![]() ��
��
��x��������P��������Q��ԭ��O������е㣬��
2��24-12x��=6x-10�����x=![]() ��
��
����������![]() ���
���![]() ���
���![]() ���ԭ��O��������P��������Q�����У���һ��ǡ���������������߶ε��е㣮
���ԭ��O��������P��������Q�����У���һ��ǡ���������������߶ε��е㣮
�������������������1������x�����������������ݼ����ҵ�·�̲�Ϊ34�����г�������⼴�ɣ���2����y����A��B��C����ľ���֮��Ϊ40����λ���ּ�Ӧλ��AB��BC֮������������ۣ�������⣮��3������ԭ��O�Ǽ�����P��������Q������е㣻��������Q�Ǽ�����P��ԭ��O������е㣻��������P��������Q��ԭ��O������е㣬����������ۼ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
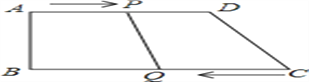
����Ŀ����ͼ,���ı���ABCD��,AD��BC, ��B��90��,AB��8�M,AD��24�M,BC��26�M,��p�ӵ�A����,��1�M/s���ٶ����D�˶�;��Q�ӵ�Cͬʱ����,��3�M/s���ٶ����B�˶�,�涨����һ�����㵽��˵�ʱ,��һ������Ҳ��ֹ֮ͣ�˶�. ���˶�ʱ��Ϊt s.
��1��tΪ��ֵʱ,�ı���PQCDΪƽ���ı���?
��2��tΪ��ֵʱ,�ı���PQCDΪ��������?���������ε�������ȣ�������ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���P(��3��m2+4m+5)����ԭ��ԳƵ���
A.��һ���� B.�ڶ����� C.�������� D.��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������������ͼ����A����3��6���������и����в��ڴ˺���ͼ���ϵ��ǣ�������
A. ��3����6�� B. ��6��3�� C. ����2��9�� D. ����9��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�н�����Ϊ�˽����2006����꼶ѧ����������������������ȡ��1000�����꼶ѧ�����м�⣬�������ʴ����Ϊ95%��������Ƹ���12�������꼶ѧ���У��������ʴ��Ĵ�Լ��_____���ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ں��� y��3-x�����н�����ȷ���ǣ� ��
A.y ��ֵ�� x �����������B.����ͼ��ؾ����㣨-1,3��
C.����ͼ������������D.�� x��1 ʱ��y��0.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����г����ʾ����¼����ǣ�������
A. ˮ������ B. ˮ��ʯ�� C. ������ D. �������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������жϣ��١�A����1��ͬλ�ǣ��ڡ�A����B��ͬ���ڽǣ��ۡ�4����1���ڴ��ǣ��ܡ�1����3��ͬλ�ǣ� ������ȷ���� ������ţ���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com