
【题目】如图,在平面直角坐标系中,A(a,0),B(0,b),且a、b满足(a﹣2)2+![]() =0.
=0.

(1)求直线AB的解析式;
(2)若点M为直线y=mx上一点,且△ABM是等腰直角三角形,求m值;
(3)过A点的直线y=kx﹣2k交y轴于负半轴于P,N点的横坐标为﹣1,过N点的直线y=![]() x﹣
x﹣![]() 交AP于点M,试证明
交AP于点M,试证明![]() 的值为定值.
的值为定值.
【答案】(1)y=﹣2x+4;(2)m的值是![]() 或
或![]() 或1.(3)
或1.(3)![]() =2.
=2.
【解析】
试题分析:(1)求出a、b的值得到A、B的坐标,设直线AB的解析式是y=kx+b,代入得到方程组,求出即可;
(2)当BM⊥BA,且BM=BA时,过M作MN⊥y轴于N,证△BMN≌△ABO(AAS),求出M的坐标即可;②当AM⊥BA,且AM=BA时,过M作MN⊥x轴于N,同法求出M的坐标;③当AM⊥BM,且AM=BM时,过M作MN⊥x轴于N,MH⊥y轴于H,证△BHM≌△AMN,求出M的坐标即可.
(3)设NM与x轴的交点为H,分别过M、H作x轴的垂线垂足为G,HD交MP于D点,求出H、G的坐标,证△AMG≌△ADH,△AMG≌△ADH≌△DPC≌△NPC,推出PN=PD=AD=AM代入即可求出答案.
解:(1)∵(a﹣2)2+![]() =0,
=0,
∴a=2,b=4,
∴A(2,0),B(0,4),
设直线AB的解析式是y=kx+b,
代入得:![]() ,
,
解得:k=﹣2,b=4,
则函数解析式为:y=﹣2x+4;
(2)如图2,分三种情况:
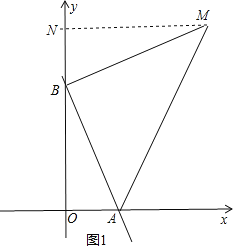
①如图1,当BM⊥BA,且BM=BA时,过M作MN⊥y轴于N,
∵BM⊥BA,MN⊥y轴,OB⊥OA,
∴∠MBA=∠MNB=∠BOA=90°,
∴∠NBM+∠NMB=90°,∠ABO+∠NBM=90°,
∴∠ABO=∠NMB,
在△BMN和△ABO中,
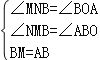 ,
,
∴△BMN≌△ABO(AAS),
MN=OB=4,BN=OA=2,
∴ON=2+4=6,
∴M的坐标为(4,6),
代入y=mx得:m=![]() ,
,
②如图2,
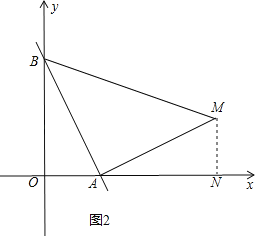
当AM⊥BA,且AM=BA时,过M作MN⊥x轴于N,△BOA≌△ANM(AAS),同理求出M的坐标为(6,2),m=![]() ,
,
③如图4,

当AM⊥BM,且AM=BM时,过M作MN⊥X轴于N,MH⊥Y轴于H,则△BHM≌△AMN,
∴MN=MH,
设M(x,x)代入y=mx得:x=mx,
∴m=1,
答:m的值是![]() 或
或![]() 或1.
或1.
(3)解:如图3,结论2是正确的且定值为2,
设NM与x轴的交点为H,过M作MG⊥x轴于G,过H作HD⊥x轴,HD交MP于D点,连接ND,
由y=![]() 与x轴交于H点,
与x轴交于H点,
∴H(1,0),
由y=![]() 与y=kx﹣2k交于M点,
与y=kx﹣2k交于M点,
∴M(3,k),
而A(2,0),
∴A为HG的中点,
∴△AMG≌△ADH(ASA),
又因为N点的横坐标为﹣1,且在y=![]() 上,
上,
∴可得N 的纵坐标为﹣k,同理P的纵坐标为﹣2k,
∴ND平行于x轴且N、D的横坐标分别为﹣1、1
∴N与D关于y轴对称,
∵△AMG≌△ADH≌△DPC≌△NPC,
∴PN=PD=AD=AM,
∴![]() =2.
=2.
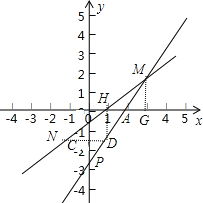


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数y=(2m-3)x+m+1经过点A(1,4)
(1)求m的值;
(2)画出此一次函数的图象;
(3)若一次函数交y轴于点B,求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 明德中学在商场购买甲、乙两种不同足球,购买甲种足球共花费3000元,购买乙种足球共花费2100元,购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元.
(1)求购买一个甲种足球、一个乙种足球各需多少元;
(2)为响应国家“足球进校园”的号召,这所学校决定再次购买甲、乙两种足球共50个,恰逢该商场对两种足球的售价进行调整,甲种足球售价比第一次购买时提高了10%,乙种足球售价比第一次购买时降低了10%.如果此次购买甲、乙两种足球的总费用不超过2950元,那么这所学校最多可购买多少个乙种足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数![]() 的图象于点B,AB=
的图象于点B,AB=![]() .
.
(1)求反比例函数的解析式;
(2)若P(![]() ,
, ![]() )、Q(
)、Q(![]() ,
, ![]() )是该反比例函数图象上的两点,且
)是该反比例函数图象上的两点,且![]() 时,
时, ![]() ,指出点P、Q各位于哪个象限?并简要说明理由.
,指出点P、Q各位于哪个象限?并简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017江苏省常州市)为了解某校学生的课余兴趣爱好情况,某调查小组设计了“阅读”、“打球”、“书法”和“其他”四个选项,用随机抽样的方法调查了该校部分学生的课余兴趣爱好情况(每个学生必须选一项且只能选一项),并根据调查结果绘制了如下统计图:
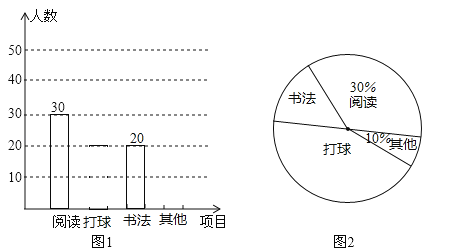
根据统计图所提供的信息,解答下列问题:
(1)本次抽样调查中的样本容量是 ;
(2)补全条形统计图;
(3)该校共有2000名学生,请根据统计结果估计该校课余兴趣爱好为“打球”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
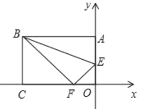
【题目】长方形纸片![]() 中,
中,![]() ,
,![]() ,把这张长方形纸片
,把这张长方形纸片![]() 如图放置在平面直角坐标系中,在边
如图放置在平面直角坐标系中,在边![]() 上取一点
上取一点![]() ,将
,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处.
处.
(1)点![]() 的坐标是____________________;点
的坐标是____________________;点![]() 的坐标是__________________________;
的坐标是__________________________;
(2)在![]() 上找一点
上找一点![]() ,使
,使![]() 最小,求点
最小,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 是直线
是直线![]() 上一个动点,设
上一个动点,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数 关系式.
的函数 关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋中装有5个只有颜色不同的球,其中3个黄球,2个黑球.
(1)求从袋中同时摸出的两个球都是黄球的概率;
(2)现将黑球和白球若干个(黑球个数是白球个数的2倍)放入袋中,搅匀后,若从袋中摸出一个球是黑球的概率是![]() ,求放入袋中的黑球的个数.
,求放入袋中的黑球的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com