
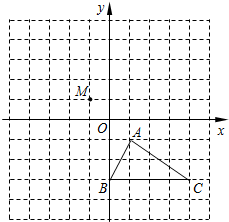
 ����ͼ��ʾ�������������У���ABC�Ķ�����ڸ���ϣ�����ƽ��ֱ������ϵ��A������Ϊ��1��-1����
����ͼ��ʾ�������������У���ABC�Ķ�����ڸ���ϣ�����ƽ��ֱ������ϵ��A������Ϊ��1��-1�������� ��1�����õ�ƽ�Ƶ��������д��A��B��C�Ķ�Ӧ��A1��B1��C1�����꣬Ȼ����㼴�ɣ�
��2�����������ص����ת�����ʷֱ���A1��B1��C1�Ķ�Ӧ��A2��B2��C2���Ӷ��õ���A2B2C2��Ȼ���������ε������ʽ�����ı��ε������
��3�������ܶ࣬����Խ���ABC������ƽ��4����λ��������ƽ��4����λ��ƽ�ƺ�ġ�ABC���A2B2C2ƴ��һ��ƽ���ı��λ�ABC������ƽ��1����λ��������ƽ��2����λ��ƽ�ƺ�ġ�ABC���A2B2C2ƴ��һ��ƽ���ı��λ�ABC������ƽ��5����λ��������ƽ��2����λ��ƽ�ƺ�ġ�ABC���A2B2C2ƴ��һ��ƽ���ı��Σ�
��� �⣺��1����ͼ����A1B1C1Ϊ������A1��-1��3����
��2����ͼ����A2B2C2Ϊ������
�ı���A1C2A2C1Ϊ���Σ��������=$\frac{1}{2}$��6��4=12��
��3�����Խ���ABC������ƽ��4����λ��������ƽ��4����λ��ƽ�ƺ�ġ�ABC���A2B2C2ƴ��һ��ƽ���ı��Σ�
���� ���⿼������ͼ-��ת�任��������ת�����ʿ�֪����Ӧ�Ƕ���ȶ�������ת�ǣ���Ӧ�߶�Ҳ��ȣ��ɴ˿���ͨ������ȵĽǣ��ڽǵı��Ͻ�ȡ��ȵ��߶εķ������ҵ���Ӧ�㣬˳�����ӵó���ת���ͼ�Σ�Ҳ������ƽ�Ʊ任��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
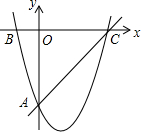 ��ͼ����֪���κ���y1=$\frac{1}{2}$x2+bx+c��ͼ����x�ύ��B��-2��0����C���㣬��y�ύ�ڵ�A��0��-6����ֱ��AC�ĺ�������ʽΪy2=mx+n
��ͼ����֪���κ���y1=$\frac{1}{2}$x2+bx+c��ͼ����x�ύ��B��-2��0����C���㣬��y�ύ�ڵ�A��0��-6����ֱ��AC�ĺ�������ʽΪy2=mx+n�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2��x��3 | B�� | -3��x��2 | C�� | x��2 | D�� | x��-3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0��1֮�� | B�� | 1��2֮�� | C�� | 2��3֮�� | D�� | 3��4֮�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com