
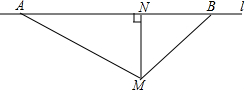
 根据道路交通管理条例的规定,在某段笔直的公路l上行驶的车辆,限速60千米/时.已知测速点M到测速区间的端点A,B的距离分别为50米、34米,M距公路l的距离(即MN的长)为30米.现测得一辆汽车从A到B所用的时间为5秒,通过计算判断此车是否超速.
根据道路交通管理条例的规定,在某段笔直的公路l上行驶的车辆,限速60千米/时.已知测速点M到测速区间的端点A,B的距离分别为50米、34米,M距公路l的距离(即MN的长)为30米.现测得一辆汽车从A到B所用的时间为5秒,通过计算判断此车是否超速. 分析 在Rt△AMN中根据勾股定理求出AN,在Rt△BMN中根据勾股定理求出BN,由AN+NB求出AB的长,根据路程除以时间得到速度,即可做出判断.
解答 解:∵在Rt△AMN中,AM=50,MN=30,
∴AN=$\sqrt{A{M}^{2}-M{N}^{2}}$=40米,
∵在Rt△MNB中,BM=34,MN=30,
∴BN=$\sqrt{B{M}^{2}-M{N}^{2}}$=16米,
∴AB=AN+NB=40+16=56(米),
∴汽车从A到B的平均速度为56÷5=11.2(米/秒),
∵11.2米/秒=40.32千米/时<60千米/时,
∴此车没有超速.
点评 此题考查了勾股定理的应用,熟练掌握勾股定理,正确求出AN与BN的长是解本题的关键.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{7}{3}$ | C. | 7 | D. | $\frac{4}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知有理数a,b,其中数a在如图的数轴上对应的点M,b是负数,且b在数轴上对应的点与原点的距离为3.5.
已知有理数a,b,其中数a在如图的数轴上对应的点M,b是负数,且b在数轴上对应的点与原点的距离为3.5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com