
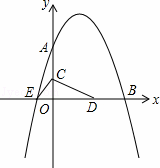
如图,已知抛物线y=﹣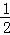 x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
(1)直接写出抛物线的解析式: ;
(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?
(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由.
解:(1)将点A(0,8)、B(8,0)代入抛物线y=﹣ x2+bx+c得:
x2+bx+c得: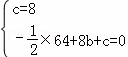 ,
,
解得:b=3,c=8,
∴抛物线的解析式为:y=﹣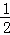 x2+3x+8,
x2+3x+8,
故答案为:y=﹣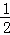 x2+3x+8;
x2+3x+8;
(2)∵点A(0,8)、B(8,0),
∴OA=8,OB=8,
令y=0,得:﹣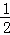 x2+3x+8=0,
x2+3x+8=0,
解得:x18,x2=2,
∵点E在x轴的负半轴上,
∴点E(﹣2,0),
∴OE=2,
根据题意得:当D点运动t秒时,BD=t,OC=t,
∴OD=8﹣t,
∴DE=OE+OD=10﹣t,
∴S=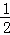 •DE•OC=
•DE•OC=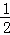 •(10﹣t)•t=﹣
•(10﹣t)•t=﹣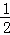 t2+5t,
t2+5t,
即S=﹣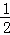 t2+5t=﹣
t2+5t=﹣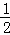 (t﹣5)2+
(t﹣5)2+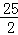 ,
,
∴当t=5时,S最大=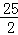 ;
;
(3)由(2)知:当t=5时,S最大=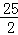 ,
,
∴当t=5时,OC=5,OD=3,
∴C(0,5),D(3,0),
由勾股定理得:CD= ,
,
设直线CD的解析式为:y=kx+b,
将C(0,5),D(3,0),代入上式得:
k=﹣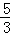 ,b=5,
,b=5,
∴直线CD的解析式为:y=﹣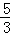 x+5,
x+5,
过E点作EF∥CD,交抛物线与点P,如图1,
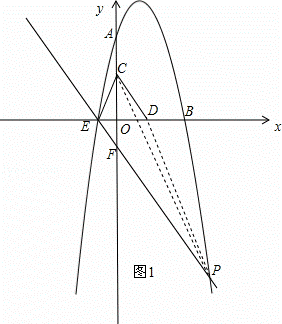
设直线EF的解析式为:y=﹣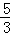 x+b,
x+b,
将E(﹣2,0)代入得:b=﹣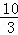 ,
,
∴直线EF的解析式为:y=﹣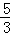 x﹣
x﹣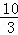 ,
,
将y=﹣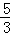 x﹣
x﹣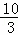 ,与y=﹣
,与y=﹣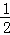 x2+3x+8联立成方程组得:
x2+3x+8联立成方程组得:
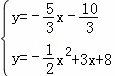 ,
,
解得: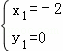 ,
,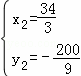 ,
,
∴P(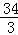 ,﹣
,﹣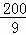 );
);
过点E作EG⊥CD,垂足为G,
∵当t=5时,S△ECD=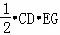 =
=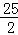 ,
,
∴EG=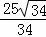 ,
,
过点D作DN⊥CD,垂足为N,且使DN=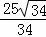 ,过点N作NM⊥x轴,垂足为M,如图2,
,过点N作NM⊥x轴,垂足为M,如图2,
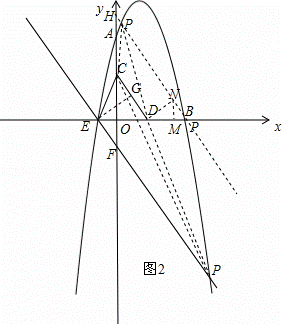
可得△EGD∽△DMN,
∴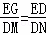 ,
,
即: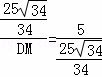 ,
,
解得:DM= ,
,
∴OM=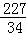 ,
,
由勾股定理得:MN=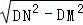 =
=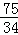 ,
,
∴N(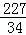 ,
,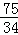 ),
),
过点N作NH∥CD,与抛物线交与点P,如图2,
设直线NH的解析式为:y=﹣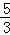 x+b,
x+b,
将N(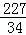 ,
,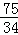 ),代入上式得:b=
),代入上式得:b=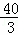 ,
,
∴直线NH的解析式为:y=﹣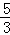 x+
x+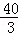 ,
,
将y=﹣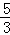 x+
x+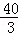 ,与y=﹣
,与y=﹣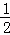 x2+3x+8联立成方程组得:
x2+3x+8联立成方程组得:
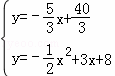 ,
,
解得: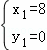 ,
,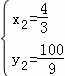 ,
,
∴P(8,0)或P(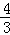 ,
,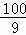 ),
),
综上所述:当△CED的面积最大时,在抛物线上存在点P(点E除外),使△PCD的面积等于△CED的最大面积,点P的坐标为:P(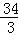 ,﹣
,﹣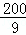 )或P(8,0)或P(
)或P(8,0)或P(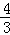 ,
,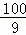 )
)


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
下列命题是假命题的是( )
|
| A. | 对角线互相垂直且相等的平行四边形是正方形 | |
|
| B. | 对角线互相垂直的矩形是正方形 | |
|
| C. | 对角线相等的菱形是正方形 | |
|
| D. | 对角线互相垂直的四边形是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:
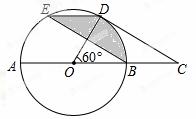
 如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为
如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为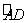 的中点,连接DE,EB.
的中点,连接DE,EB.
(1)求证:四边形BCDE是平行四边形;
(2)已知图中阴影部分面积为6π,求⊙O的半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
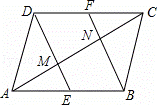
如图,在▱ABCD中,E、F分别是AB、CD的中点.
(1)求证:四边形EBFD为平行四边形;
(2)对角线AC分别与DE、BF交于点M、N,求证:△ABN≌△CDM.
查看答案和解析>>
科目:初中数学 来源: 题型:
某市户籍人口1694000人,则该市户籍人口数据用科学记数法可表示为( )
A. 1.694×104人 B. 1.694×105人 C. 1.694×106人 D. 1.694×107人
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在矩形OABC中,OA=8,OC=4,沿对角线OB折叠后,点A与点D重合,OD与BC交于点E,则点D的坐标是( )
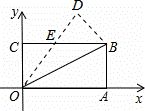
A. (4,8) B. (5,8) C. (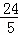 ,
, ) D. (
) D. (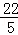 ,
,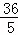 )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
经统计分析,某市跨河大桥上的车流速度v(千米/小时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为80千米/时,研究表明:当20≤x≤220时,车流速度v是车流密度x的一次函数.
(1)求大桥上车流密度为100辆/千米时的车流速度;
(2)在交通高峰时段,为使大桥上的车流速度大于40千米/小时且小于60千米/时,应控制大桥上的车流密度在什么范围内?
(3)车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.求大桥上车流量y的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com