
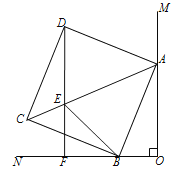
【题目】如图,∠MON=90°,正方形ABCD的顶点A、B分别在OM、ON上,AB=13,OB=5,E为AC上一点,且∠EBC=∠CBN,直线DE与ON交于点F.
(1)求证BE=DE;
(2)判断DF与ON的位置关系,并说明理由;
(3)△BEF的周长为 .
【答案】(1)见解析;(2)DF⊥ON,理由见解析;(3)24
【解析】
(1)根据正方形的性质证明△BCE≌△DCE即可;
(2)由第一题所得条件和已知条件可推出∠EDC=∠CBN,再利用90°的代换即可证明;
(3)过D点作DG垂直于OM,交点为G,结合已知条件推出DF和BF的长,再根据第一题结论得出△BEF的周长等于DF加BF即可得出答案.
解:(1)证明:∵四边形ABCD正方形,
∴CA平分∠BCD,BC=DC,
∴∠BCE=∠DCE=45°,
∵CE=CE,
∴△BCE≌△DCE(SAS);
∴BE=DE;
(2)DF⊥ON,理由如下:

∵△BCE≌△DCE,
∴∠EBC=∠EDC,
∵∠EBC=∠CBN,
∴∠EDC=∠CBN,
∵∠EDC+∠1=90°,∠1=∠2,
∴∠2+∠CBN=90°,
∴∠EFB=90°,即DF⊥ON;
(3)过D点作DG垂直于OM,交点为G,
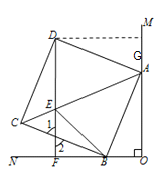
∵四边形ABCD是正方形,
∴AD=AB,∠BAD=90°,
∴∠DAG+∠BAO=90°,
∵∠ABO+∠BAO=90°,
∴∠DAG=∠ABO,
又∵∠MON=90°,DG⊥OM,
∴△ADG≌△ABO,
∴DM=AO,GA=OB=5,
∵AB=13,OB=5,
根据勾股定理可得AO=12,
由(2)可知DF⊥ON,
又∵∠MON=90°,DG⊥OM,
∴四边形OFDM是矩形,
∴OF=DG=AO=12,DF=OM=17,
由(1)可知BE=DE,
∴△BEF的周长=DF+BF=17+(12-5)=24.


科目:初中数学 来源: 题型:
【题目】在学习完《有理数》后,小奇对运算产生了浓厚的兴趣.借助有理数的运算,定义了一种新运算“⊕”,规则如下:a⊕b=a×b+2×a.
(1)求2⊕(﹣1)的值;
(2)求﹣3⊕(﹣4⊕![]() )的值;
)的值;
(3)试用学习有理数的经验和方法来探究这种新运算“⊕”是否具有交换律?请写出你的探究过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数![]() (k>0)的图象经过BC边的中点D(3,1).
(k>0)的图象经过BC边的中点D(3,1).
(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某区初中生一周课外阅读时长的情况,随机抽取部分中学生进行调查,根据调查结果,将阅读时长分为四类:2小时以内,2~4小时(含2小时),4~6小时(含4小时),6小时及以上,并绘制了如图所示不完整的统计图.

(1)本次调查共随机抽取了 名学生;
(2)补全条形统计图;
(3)扇形统计图中,课外阅读时长“4~6小时”对应的圆心角度数为 ![]() ;
;
(4)若该区共有10 000名初中生,估计该地区中学生一周课外阅读时长不少于4小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(1)﹣7﹣1;
(2)(﹣3)+(﹣5)﹣(+11)﹣(﹣17);
(3)﹣3+8﹣7;
(4)(![]() )×(﹣24);
)×(﹣24);
(5)(![]() )×(﹣12);
)×(﹣12);
(6)(﹣0.1)﹣(﹣8![]() )+(﹣11
)+(﹣11![]() )﹣(﹣
)﹣(﹣![]() );
);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图像经过第二象限内的点
的图像经过第二象限内的点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() 的面积为2.若直线
的面积为2.若直线![]() 经过点
经过点![]() ,并且经过反比例函数
,并且经过反比例函数![]() 的图像上另一点
的图像上另一点![]() .
.
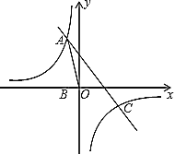
(1)求反比例函数![]() 与直线
与直线![]() 的解析式;
的解析式;
(2)连接![]() ,求
,求![]() 的面积;
的面积;
(3)不等式![]() 的解集为_________
的解集为_________
(4)若![]() 在
在![]()
![]() 图像上,且满足
图像上,且满足![]() ,则
,则![]() 的取值范围是_________.
的取值范围是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正![]() 内接于
内接于![]() 是劣弧BC上任意一点,PA与BC交于点E,有如下结论:
是劣弧BC上任意一点,PA与BC交于点E,有如下结论:
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() 图中共有6对相似三角形.
图中共有6对相似三角形.
其中,正确结论的个数为![]()
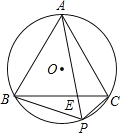
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com