
【题目】如图1,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() )两点与x轴,y轴分别交于A、B(0,2)两点,如果
)两点与x轴,y轴分别交于A、B(0,2)两点,如果![]() 的面积为6.
的面积为6.

(1)求点A的坐标;
(2)求一次函数和反比例函数的解析式;
(3)如图2,连接DO并延长交反比例函数的图象于点E,连接CE,求点E的坐标和![]() 的面积
的面积
【答案】(1)A(﹣4,0);(2)![]() ,
,![]() ;(3)
;(3)![]() ,8
,8
【解析】
(1)由三角形面积求出OA=4,即可求得A(-4,0).
(2)利用待定系数法即可求出一次函数的解析式,进而求得C点的坐标,把C点的坐标代入![]() ,求出m的值,得到反比例函数的解析式;
,求出m的值,得到反比例函数的解析式;
(3)先联立两函数解析式得出D点坐标,根据中心对称求得E点的坐标,然后根据三角形的面积公式计算△CED的面积即可.
(1)如图1,
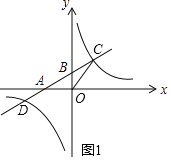
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 的面积为6,
的面积为6,
∴![]() ,
,
∵![]() ,
,
∴OA=4,
∴A(﹣4,0);
(2)如图1,把![]() 代入
代入![]() 得
得![]() ,
,
解得![]() ,
,
∴一次函数的解析式为![]() ,
,
把![]() 代入得,
代入得,![]() ,
,
∴![]() ,
,
∵点C在反比例函数![]() 的图象上,
的图象上,
∴m=2×3=6,
∴反比例函数的解析式为![]() ;
;
(3)如图2,作![]() 轴于F,
轴于F,![]() 轴于H,
轴于H,
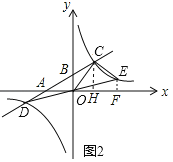
解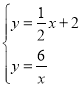 ,得
,得![]() ,
,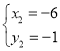 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() =
=![]()


科目:初中数学 来源: 题型:
【题目】已知:矩形ABCD中,AB=10,AD=8,点E是BC边上一个动点,将△ABE沿AE折叠得到△AB′E。
(1)如图(1),点G和点H分别是AD和AB′的中点,若点B′在边DC上。
①求GH的长;
②求证:△AGH≌△B′CE;
(2)如图(2),若点F是AE的中点,连接B′F,B′F∥AD,交DC于I。
①求证:四边形BEB′F是菱形;
②求B′F的长。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,![]() ,点E、F分别在边AD和边BC上,且
,点E、F分别在边AD和边BC上,且![]() ,动点P、Q分别从A、C两点同时出发,点P自A→F→B方向运动,点Q自C→D→E→C方向运动若点P、Q的运动速度分别为1cm/s,3cm/s,设运动时间为
,动点P、Q分别从A、C两点同时出发,点P自A→F→B方向运动,点Q自C→D→E→C方向运动若点P、Q的运动速度分别为1cm/s,3cm/s,设运动时间为![]() ,当A 、C、P、Q四点为顶点的四边形是平行四边形时则t= ________________
,当A 、C、P、Q四点为顶点的四边形是平行四边形时则t= ________________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形ABCD中,点E、F、G分别是边AD、AB、BC的中点,连接EP、FG.
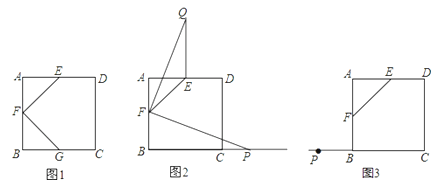
(1)如图1,直接写出EF与FG的关系____________;
(2)如图2,若点P为BC延长线上一动点,连接FP,将线段FP以点F为旋转中心,逆时针旋转90°,得到线段FH,连接EH.
①求证:△FFE≌△PFG;②直接写出EF、EH、BP三者之间的关系;
(3)如图3,若点P为CB延长线上的一动点,连接FP,按照(2)中的做法,在图(3)中补全图形,并直接写出EF、EH、BP三者之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
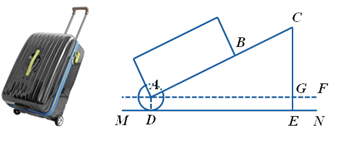
【题目】有一只拉杆式旅行箱(图1),其侧面示意图如图2所示.已知箱体长AB=50cm,拉杆![]() 的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.
的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.
设AF∥MN.
(1)求⊙A的半径长;
(2)当人的手自然下垂拉旅行箱时,人感到较为舒服.某人将手自然下垂在C端拉旅行箱时,CE为80cm,![]() =64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:
=64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一动点从原点![]() 出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到
出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到![]() (0,1),
(0,1),![]() (1,1),
(1,1),![]() (1,0),
(1,0),![]() (2,0),…那么点
(2,0),…那么点![]() 的坐标为__________.
的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有个填写运算符号的游戏:在“![]() ”中的每个□内,填入
”中的每个□内,填入![]() 中的某一个(可重复使用),然后计算结果.
中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若请推算![]() □内的符号;
□内的符号;
(3)在“![]() ”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
查看答案和解析>>
科目:初中数学 来源: 题型:
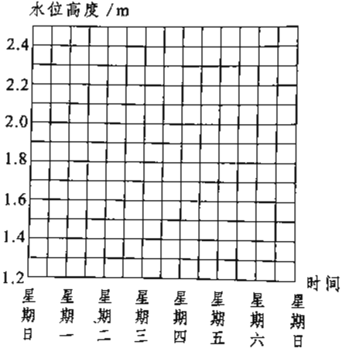
【题目】下表是一个水文站在雨季对某条河一周内水位变化情况的记录.其中,水位上升用正数表示,水位下降用负数表示(水位变化的单位:m).
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
变化 | +0.4 | -0.3 | -0.4 | -0.3 | +0.2 | +0.2 | +0.1 |
注:①表中记录的数据为每天12时的水位与前一天12时的水位的变化量.
②上周日12时的水位高度为2m.
(1)请你通过计算说明本周末水位是上升了还是下降了;
(2)用折线图表示本周每天的水位,并根据折线图说明水位在本周内的升降趋势.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道:|5﹣(﹣2)|表示5与﹣2之差的绝对值,实际上也可理解为5与﹣2两数在数轴上所对应的两点之间的距离.请你借助数轴进行以下探索:
![]()
(1)数轴上表示5与﹣2两点之间的距离是 ;
(2)数轴上表示x与2的两点之间的距离可以表示为 ;
(3)同理|x+3|+|x﹣1|表示数轴上有理数x所对应的点到﹣3和1所对应的点的距离之和,请你找出所有符合条件的整数x,使得|x+3|+|x﹣1|=4,这样的整数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com