练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．小丽家在铺设地板时，用的是边长相等的三种正多边形，已知第一种正多边形的一个内角是120°，另一种是正方形，而且铺地板时，在一个顶点处，这三种正多边形都是一个，则第三种正多边形应是正12边形．

    分析 正多边形的组合能否进行平面镶嵌，关键是看位于同一顶点处的几个角之和能否为360°．若能，则说明可以进行平面镶嵌；反之，则说明不能进行平面镶嵌．

    解答 解：∵正方形的一个内角度数为180°-360°÷4=90°，正六边形的一个内角度数为180°-360°÷6=120°，
    ∴需要的多边形的一个内角度数为360°-90°-120°=150°，
    ∴需要的多边形的一个外角度数为180°-150°=30°，
    ∴第三个正多边形的边数为360÷30=12．
    故答案为：12．

    点评 此题主要考查了平面镶嵌，关键是掌握多边形镶嵌成平面图形的条件：同一顶点处的几个内角之和为360°；正多边形的边数为360÷一个外角的度数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    9．观察下列算式，用你所发现的规律得出22010的末位数字是（　　）
    21=2，22=4，23=8，24=16，25=32，26=64，27=128，28=256，…
    A．2B．4C．6D．8

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，在?ABCD中，∠BCD=120°，分别以BC和CD为边作等边△BCE和等边△CDF．
    求证：AE=AF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

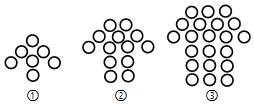    7．下列图形都是由两样大小的小圆圈按一定规律组成的，其中第①个图形中一共有7个小圆圈，第②个图形中一共有13个小圆圈，第③个图形中一共有21个小圆圈，…，按此规律排列，则第⑧个图形中小圆圈的个数为（　　）
    A．68B．88C．91D．93

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

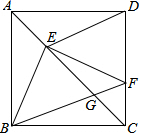    14．如图，正方形ABCD的边长为1，点E、F分别在AC、DC上，若EC=BC，EF⊥BE，BF与EC交于点G，则$\frac{EG}{CG}$=$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．定点O、P的距离是5，以点O为圆心，一定的长为半径画圆⊙O，过点P作⊙O的两条切线，切点分别是B、C，则线段BC的最大值是5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

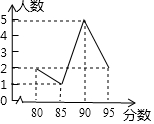    11．在一次“班班有诗词”竞赛活动中，某班10名学生的成绩折线统计图如图所示，若随机从这10名学生中抽取一人，则抽中概率最大的学生得分是90分．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．已知，∠ABC=48°，P是∠ABC内一定点，D、E分别是射线BA、BC上的点，当△PDE的周长最小时，∠DPE的度数是84°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．若数据8，9，7，8，x，2的平均数是7，则这组数据的众数是8．

    查看答案和解析>>

    同步练习册答案