
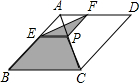
 如图所示,菱形ABCD的对角线的长分别为4和6,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是6.
如图所示,菱形ABCD的对角线的长分别为4和6,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是6. 分析 根据题意可得阴影部分的面积等于△ABC的面积,因为△ABC的面积是菱形面积的一半,根据已知可求得菱形的面积则不难求得阴影部分的面积.
解答 解:设AP与EF相交于O点.
∵四边形ABCD为菱形,
∴BC∥AD,AB∥CD.
∵PE∥BC,PF∥CD,
∴PE∥AF,PF∥AE.
∴四边形AEPF是平行四边形.
∴S△POF=S△AOE.
即阴影部分的面积等于△ABC的面积.
∵△ABC的面积等于菱形ABCD的面积的一半,
菱形ABCD的面积=$\frac{1}{2}$AC•BD=12,
∴图中阴影部分的面积为12÷2=6.
故答案为:6.
点评 本题主要考查了菱形的面积的计算方法,根据菱形是中心对称图形,得到阴影部分的面积等于菱形面积的一半是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | F+V-E=2 | B. | F+E-V=2 | C. | E+V-F=2 | D. | E-V-F=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 正方形ABCD的边长为1,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S2,…按此规律继续下去,则S9的值为( )
正方形ABCD的边长为1,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S2,…按此规律继续下去,则S9的值为( )| A. | ${({\frac{1}{2}})^9}$ | B. | ${({\frac{1}{2}})^8}$ | C. | ${({\frac{{\sqrt{2}}}{2}})^9}$ | D. | ${({\frac{{\sqrt{2}}}{2}})^8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
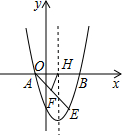 如图,抛物线y=x2+bx+c经过点A(-1,0),B(3,0).
如图,抛物线y=x2+bx+c经过点A(-1,0),B(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
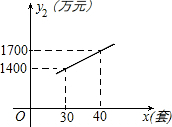 某企业生成一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=190-2x.月产量x(套)与生成总成本y2(万元)存在如图所示的函数关系.
某企业生成一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=190-2x.月产量x(套)与生成总成本y2(万元)存在如图所示的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com