练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

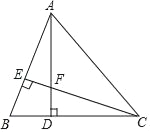
    【题目】如图所示，在△ABC中，AD⊥BC于D，CE⊥AB于E，AD与CE交于点F，且AD=CD．

    （1）求证：△ABD≌△CFD；

    （2）已知BC=7，AD=5，求AF的长．

    【答案】（1）证明见解析；（2）3.

    【解析】

    （1）易由，可证△ABD≌△CFD（AAS）；

    （2）由△ABD≌△CFD，得BD=DF，所以BD=BC﹣CD=2，所以AF=AD﹣DF=5﹣2．

    （1）证明：∵AD⊥BC，CE⊥AB，

    ∴∠ADB=∠CDF=∠CEB=90°，

    ∴∠BAD+∠B=∠FCD+∠B=90°，

    ∴∠BAD=∠OCD，

    在△ABD和CFD中，

    ，

    ∴△ABD≌△CFD（AAS），

    （2）∵△ABD≌△CFD，

    ∴BD=DF，

    ∵BC=7，AD=DC=5，

    ∴BD=BC﹣CD=2，

    ∴AF=AD﹣DF=5﹣2=3．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，O为坐标原点，点A(-a，a)(a>0)，点B(-a-4，a+3)，C为该直角坐标系内的一点，连结AB，OC．若AB∥OC且AB=OC，则点C的坐标为________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在△中，＞，∥=,点在 边上，连接，则添加下列哪一个条件后，仍无法判定△与△全等（　　）

    A. ∥ B. C. ∠=∠ D. ∠=∠

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一次函数y=kx+b的图象过P（1，4），Q（4，1）两点，且与x轴交于A点．

    （1）求此一次函数的解析式；

    （2）求△POQ的面积；

    （3）已知点M在x轴上，若使MP+MQ的值最小，

    求点M的坐标及MP+MQ的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=x2﹣（2m+1）+（ m2﹣1）．
    （1）求证：不论m取什么实数，该二次函数图象与x轴总有两个交点；
    （2）若该二次函数图象经过点（2m﹣2，﹣2m﹣1），求该二次函数的表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠BAD=∠CAE=90°，AB=AD，AE=AC，AF⊥CB，垂足为F．

    （1）求证：△ABC≌△ADE；（图1）

    （2）求∠FAE的度数；（图1）

    （3）如图2，延长CF到G点，使BF=GF，连接AG．求证：CD=CG；并猜想CD与2BF+DE的关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】函数yl=x（x≥0）， （x＞0）的图象如图所示，则结论： ①两函数图象的交点A的坐标为（3，3）；
    ②当x＞3时，y2＞y1；
    ③当x=1时，BC=8；
    ④当x逐渐增大时，yl随着x的增大而增大，y2随着x的增大而减小．
    其中正确结论的序号是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

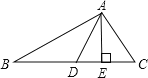
    【题目】已知如图所示 AD、AE分别是△ABC的中线、高，且AB=5cm，AC=3cm，,则△ABD与△ACD的周长之差为_________，△ABD与△ACD的面积关系为_________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，对角线AC=2 ，E为BC边上一点，BC=3BE，将矩形ABCD沿AE所在的直线折叠，B点恰好落在对角线AC上的B′处，则AB= ．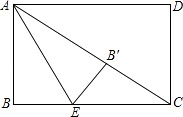

    查看答案和解析>>

    同步练习册答案